Mechanical analogy

import numpy as np
import matplotlib.pyplot as plt

def Vm(a, Om):
    return -0.5 * Om/a

def Vk(Om, Or, OL):
    return 0.5*((1-Om-Or-OL))

def Vr(a, Or):
    return -0.5*Or/a**2

def VL(a, OL):
    return -0.5*OL*a**2

def Veff(a, Om, Or, OL):
    return Vm(a,Om) + Vr(a,Or) + VL(a,OL)

def plot_Vs(Om, Or, OL, ylim=None):
    a=np.linspace(0.1, 10, 500)
    fig = plt.figure()
    plt.plot(a, Vm(a, Om), label=r"$V_{\Omega_m}(a)$")
    plt.plot(a, Vr(a, Or), label=r"$V_{\Omega_r}(a)$")
    plt.plot(a, VL(a, OL), label=r"$V_{\Omega_\Lambda}(a)$")
    plt.plot(a, Veff(a, Om, Or, OL), "r-", lw=2, label=r"$V_{\mathrm{eff}}(a)$")
    plt.axvline(1, color="k", label="today")
    plt.axhline(Vk(Om,Or,OL), color="b", label=r"$E_{\mathrm{tot}}=\Omega_k^0/2$")
    plt.xscale("log")
    plt.legend()
    plt.xlabel("$a$")
    plt.ylim(ylim)
    plt.grid()
    plt.show()

Om, Or, OL = 1., 0, 0
plot_Vs(Om, Or, OL)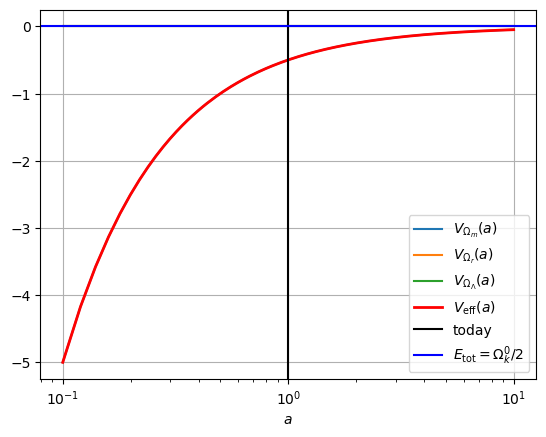

Om, Or, OL = 1.5, 0, 0
plot_Vs(Om, Or, OL)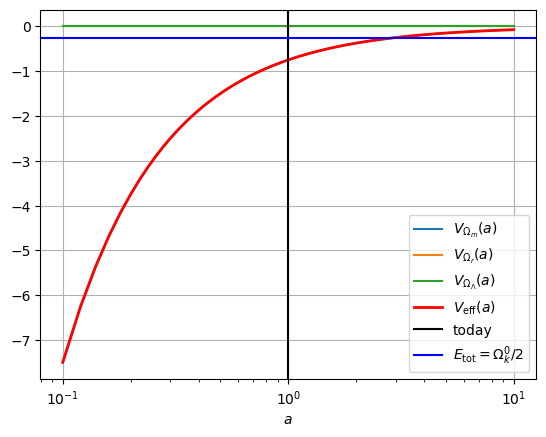

Om, Or, OL = 0.5, 0, 0
plot_Vs(Om, Or, OL)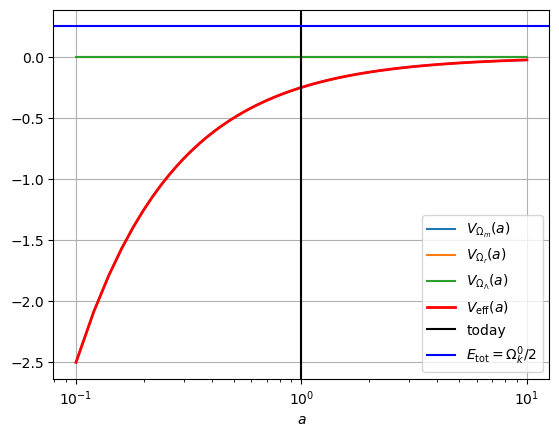

Om, Or, OL = 1, 0, 0.5
plot_Vs(Om, Or, OL, ylim=(-6,1))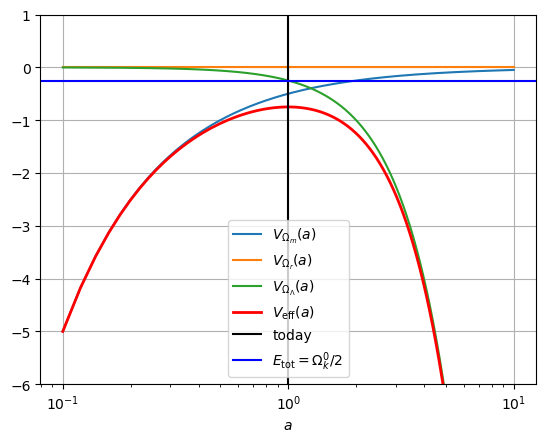

Om, Or, OL = 0.3, 0, 0.7
plot_Vs(Om, Or, OL, ylim=(-3, 1))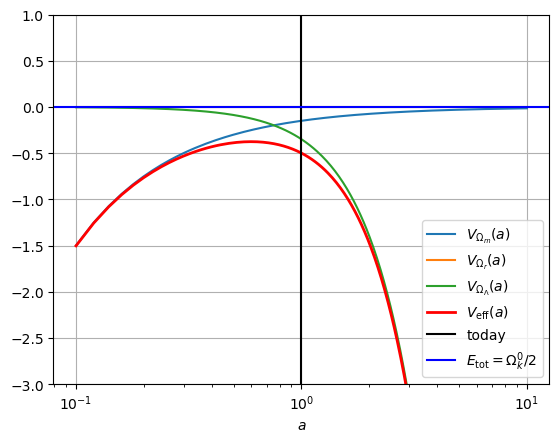

Om, Or, OL = 0.3, 0, 0.5
plot_Vs(Om, Or, OL, ylim=(-3, 1))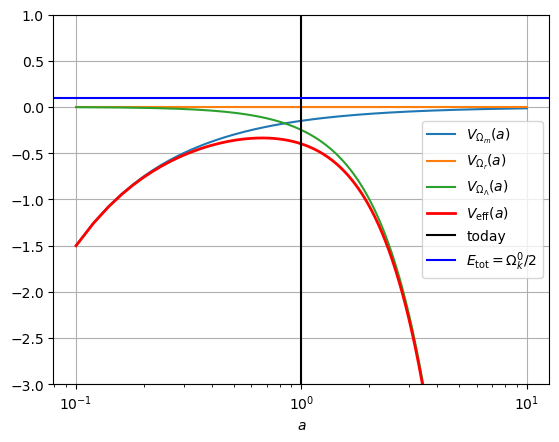

Om, Or, OL = 0.3, 0, 1.5
plot_Vs(Om, Or, OL, ylim=(-3, 1))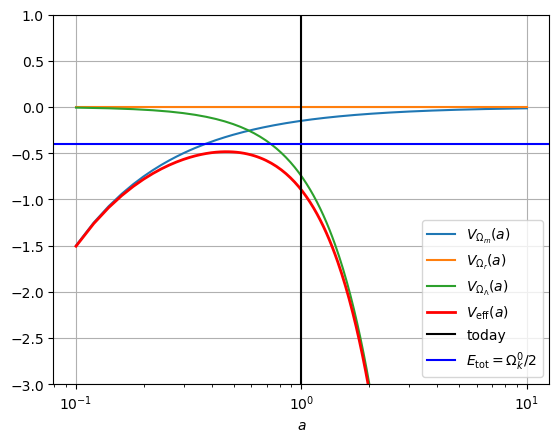

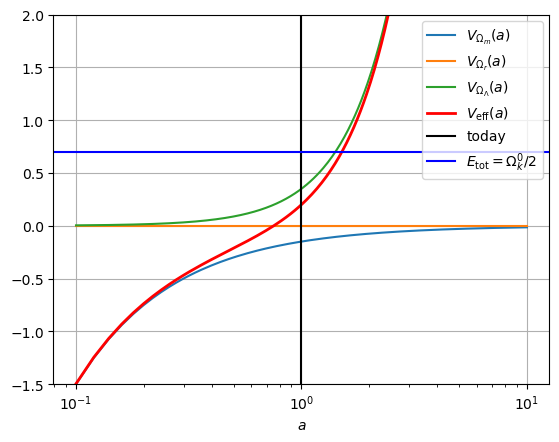
Om, Or, OL = 0.3, 0, -0.7
plot_Vs(Om, Or, OL, ylim=(-1.5, 2))