Skip to article frontmatterSkip to article content

Type Ia supernovae

Authors
Affiliations
Université Paris-Saclay
IJCLab
Université Paris-Saclay
IJCLab

1A simple Hubble diagram

The luminosity distance DL(z)D_L(z) is defined as follows:

DL(z)={(1+z)cH0−Ωk0sin⁡[H0−Ωk0∫0zdzH(z)] if k=+1(1+z)∫0zcdzH(z) if k=0(1+z)cH0Ωk0sinh⁡[H0Ωk0∫0zdzH(z)] if k=−1D_L(z) = \left\lbrace\begin{array}{cl} \displaystyle{\frac{(1+z)c}{H_0\sqrt{-\Omega_k^0}}\sin\left[H_0\sqrt{-\Omega_k^0}\int_0^z\frac{dz}{H(z)}\right]} & \text{ if } k=+1 \\ \displaystyle{(1+z)\int_0^z\frac{cdz}{H(z)}} & \text{ if } k=0 \\ \displaystyle{\frac{(1+z)c}{H_0\sqrt{\Omega_k^0}}\sinh\left[H_0\sqrt{\Omega_k^0}\int_0^z\frac{dz}{H(z)}\right] } & \text{ if } k=-1 \end{array} \right.
(1)

In the joined data file, the most recent type Ia supernovae measurements from SNLS collaboration have been reported Betoule et al. 2014. 740 good quality supernovae are present with their name, their redshift zz (zcmb) and their rest-frame BB band peak magnitude mB∗m_B^* (mb) with its uncertainty δmB∗\delta m_B^* (dmb). They are sorted by redshift in ascending order.

SNLS 3-year Hubble diagram Conley et al. 2011.
  • First, initialize the notebook and make the plot mB∗(z)m_B^*(z) so as it looks like the one in figure above.
# initialisation og the notebook
import numpy as np
import matplotlib.pylab as plt
import matplotlib
import matplotlib.cm as cm
from astropy.cosmology import LambdaCDM
import astropy.units as u

%matplotlib inline
import pandas as pd

df = pd.read_csv("data/sne_data_zsorted.txt", delimiter="\t")
df
Loading...
fig = plt.figure()
plt.errorbar(x=df['zcmb'],y=df['mb'],xerr=np.abs(df['dz']),yerr=df['dmb'],fmt='o',color='b',markersize=1)
plt.xlabel('$z$',size='14')
plt.xlim([0.000,1.4])
plt.ylabel('$m^*_{B}$ [mag]',size='14')
plt.grid()
plt.show()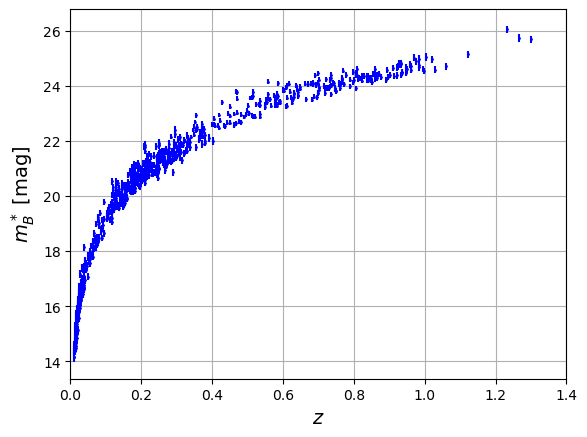
<Figure size 640x480 with 1 Axes>
  • As the cosmological models that fit data are compatible with a flat universe, in the array dL compute the dL(z)d_L(z) luminosity distance assuming a flat universe. Then set mag array as:
mB,model∗=5log⁡10dL(z)+Mm^*_{B,\rm model} = 5 \log_{10} d_L(z) + \mathcal{M}
(2)

Set M\mathcal{M} with the M variable and the value you found in the previous exercise. Superimpose mB,model∗m^*_{B,\rm model} on the Hubble diagram and comment.

cosmo = LambdaCDM(Om0=0.3, Ode0=0.7, H0=70)
MB = -19.08
M = MB - 5*np.log10(10*u.parsec / cosmo.hubble_distance)
print(M)
24.078613314568358

z = np.linspace(0.01, 1.4, 50)

fig = plt.figure()
cosmo = LambdaCDM(Om0=0.3, Ode0=0.7, H0=75)
plt.plot(z, cosmo.distmod(z),'b-',lw=2, label=f"$\Omega_m^0=0.3$, $\Omega_\Lambda^0=0.7$, $H_0=75\,$km/s/Mpc")
cosmo = LambdaCDM(Om0=0.3, Ode0=0.7, H0=65)
plt.plot(z, cosmo.distmod(z),'b--',lw=2, label=f"$\Omega_m^0=0.3$, $\Omega_\Lambda^0=0.7$, $H_0=65\,$km/s/Mpc")
cosmo = LambdaCDM(Om0=1, Ode0=0., H0=75)
plt.plot(z, cosmo.distmod(z),'r-',lw=2, label=f"$\Omega_m^0=1$, $\Omega_\Lambda^0=0$, $H_0=75\,$km/s/Mpc")
plt.xlabel('$z$',size=14)
plt.xlim([0.000,1.4])
plt.ylabel('$\mu(z)$',size=14)
plt.legend(fontsize='14')
plt.grid()
plt.show()
<Figure size 640x480 with 1 Axes>
def mu_f(z, OmegaM, OmegaL, M, H0=70):
    cosmo = LambdaCDM(Om0=OmegaM, Ode0=OmegaL, H0=H0)
    return 5*np.log10(cosmo.luminosity_distance(z)/cosmo.hubble_distance) + M

z = np.linspace(0.01, 1.4, 50)
mu = mu_f(z, 0.3, 0.7, M)
  • To check the quality of the fit, first complete the delta array with mB∗−mB,model∗m_B^* - m^*_{B,\rm model} and compute χ2\chi^2s for each SNIa in array chisq. In the fit control table, in cell RMS compute the standard deviation of the delta array. In cell total_chisq compute the total χ2\chi^2 as the sum of the chisq array. Compare the latter with the number of measurements.
from scipy.optimize import curve_fit

pval, pcov = curve_fit(mu_f, df['zcmb'], df['mb'], sigma=df['dmb'], p0=(0.3,0.7,24), absolute_sigma=True)
print(pval)
[ 0.3748276   0.32227609 24.10833295]

#### To complete
delta =  df['mb'] - mu_f(df['zcmb'], *pval)
chisq =  delta**2/df['dmb']**2

# Fit control table
RMS =                 np.std(delta)
total_chisq =         np.sum(chisq)
####

print('RMS: ',RMS)
print('Total chisq: ',total_chisq)
RMS:  0.2804584476461635
Total chisq:  4578.591303886714

fig = plt.figure()
plt.errorbar(x=df['zcmb'],y=df['mb'],xerr=np.abs(df['dz']),yerr=df['dmb'],fmt='.',capsize=2,lw=1,color='k',markersize=1)
plt.plot(z, mu_f(z, *pval),'r-',lw=2, label=f"$\Omega_m^0={pval[0]:.2f}$"+"\n"+f"$\Omega_\Lambda^0={pval[1]:.2f}$")
plt.xlabel('$z$',size=14)
plt.xlim([0.000,1.4])
plt.ylabel('$m^*_{B}(z)$',size=14)
plt.legend()
plt.grid()
plt.show()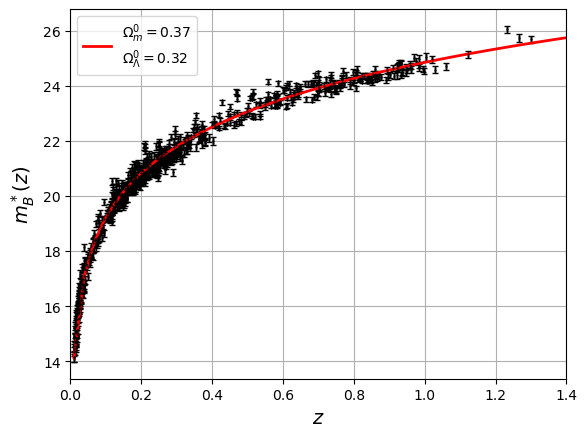
<Figure size 640x480 with 1 Axes>
fig = plt.figure()
plt.errorbar(x=df['zcmb'],y=delta,xerr=np.abs(df['dz']),yerr=df['dmb'],fmt='.',color='b',markersize=1)
plt.plot(z,np.zeros_like(z),'r-',lw=2)
plt.xlabel('$z$',size='14')
plt.xlim([0.000,1.4])
plt.ylabel('$m^{*}_{B}(z) - m^{*}_{B,\mathrm{model}}$ [mag]',size='14')
plt.grid()
plt.show()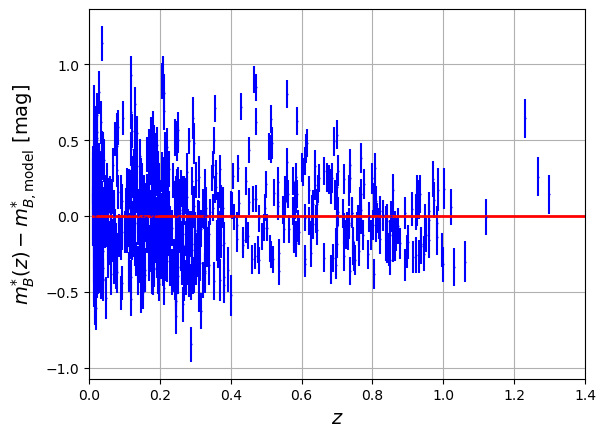
<Figure size 640x480 with 1 Axes>
fig = plt.figure()
sc = plt.scatter(x=df['zcmb'], y=delta, marker='+', s=15, linewidths=2, c=df['x1'], cmap=plt.colormaps['Blues'])
#create colorbar according to the scatter plot
clb = plt.colorbar(sc, extend='both')
clb.set_label(label="$x_1$", size=14)

#convert third variable to a color tuple using the colormap used for scatter
norm = matplotlib.colors.Normalize(vmin=min(df['x1']), vmax=max(df['x1']), clip=True)
mapper = cm.ScalarMappable(norm=norm, cmap='Blues')
color_l = np.array([(mapper.to_rgba(v)) for v in df['x1']])

#loop over each data point to plot
for x, y, e, color in zip(df['zcmb'], delta, df['dmb'], color_l):
    plt.plot(x, y, 'o', color=color)
    plt.errorbar(x, y, e, lw=1, capsize=2, color=color)

plt.plot(z,np.zeros_like(z),'r-',lw=2)
plt.xlabel('$z$',size='14')
plt.xlim([0.000,1.4])
plt.ylabel('$m^{*}_{B} - [\mu(z) + M_B]$ [mag]',size='14')
plt.grid()
plt.show()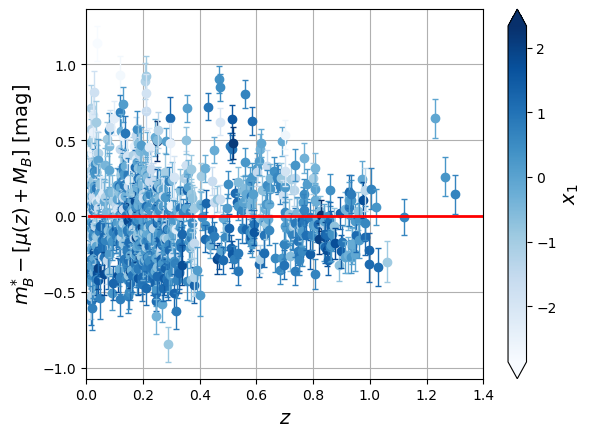
<Figure size 640x480 with 2 Axes>
fig = plt.figure()
sc = plt.scatter(x=df['zcmb'],y=delta, marker='+', s=15, linewidths=2, c=df['color'], cmap=plt.colormaps['Reds'])
#create colorbar according to the scatter plot
clb = plt.colorbar(sc, extend='both')
clb.set_label(label="$c$", size=14)

#convert third variable to a color tuple using the colormap used for scatter
norm = matplotlib.colors.Normalize(vmin=min(df['color']), vmax=max(df['color']), clip=True)
mapper = cm.ScalarMappable(norm=norm, cmap='Reds')
color_l = np.array([(mapper.to_rgba(v)) for v in df['color']])

#loop over each data point to plot
for x, y, e, color in zip(df['zcmb'], delta, df['dmb'], color_l):
    plt.plot(x, y, 'o', color=color)
    plt.errorbar(x, y, e, lw=1, capsize=2, color=color)

plt.plot(z,np.zeros_like(z),'r-',lw=2)
plt.xlabel('$z$',size='14')
plt.xlim([0.000,1.4])
plt.ylabel('$m^{*}_{B} - [\mu(z) + M_B]$ [mag]',size='14')
plt.grid()
plt.show()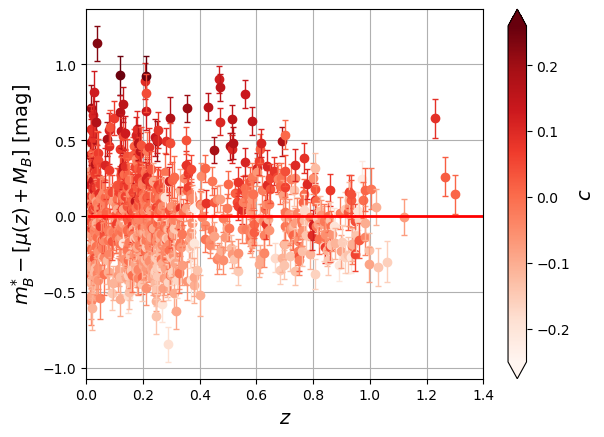
<Figure size 640x480 with 2 Axes>
  • Comment the value of total_chisq and RMS.

The total value of total_chisq is huge compared to 740 : it means that the fit is bad even for a good-looking fit on the plot. The spread of data around the model is too important: RMS is around 0.3 mag.

2Corrected magnitudes

Actually, the type Ia supernovae are not so standard. They have little systematic variability that depends on their color or their time length (Astier et al. 2001). For instance, the longer is the supernovae the brighter it is also (the brighter-slower rule). These systematic bias can be removed to make more standard candles and increase the quality of the data sample.

In the data file, the color column gives the color in the B−VB-V band and the “stretch” parameter x1 measures the duration of the supernova. They are given with their uncertainties.

  • First, make a scatter plot of mb-mag versus x1. Add the uncertainties and fit the plot by a line: mB∗−mag ≡ α x1m_B^*-\texttt{mag}\, \equiv \, \alpha\, \texttt{x1} . Print the equation of the fit and comment it.
#### To complete
fit,cov = np.polyfit(  x=df['x1'],y=delta,deg=1,cov=True,w=1/df['dmb'])
alpha =            fit[0]
alpha_err =        np.sqrt(cov[0,0])
####

line_alpha = np.polyval(fit, df['x1'])
print('Alpha value: ',alpha,' +/- ',alpha_err)
Alpha value:  -0.1128704517377774  +/-  0.009782982675423414

fig = plt.figure()
ax = fig.add_subplot(111)
plt.errorbar(x=df['x1'], y=delta, xerr=df['dx1'],yerr=df['dmb'], fmt='.',color='b',markersize=1)
plt.plot(df['x1'], line_alpha, 'r-', lw=2)
ax.set_xlabel('$\mathtt{x1}$', size='14')
ax.set_ylabel('$m^{*}_{B}(z)- m^{*}_{B,\mathrm{model}}$ [mag]', size='14')
plt.show()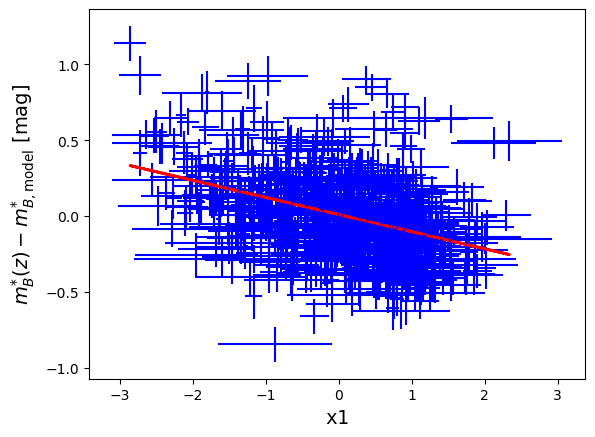
<Figure size 640x480 with 1 Axes>

We see a systematic trend between the data points: it means that the supernovae are not so standard and that their magnitude depends on un-modelled physical properties. The fit gives mB∗−mag≈0.125 x1m_B^*-\texttt{mag} \approx 0.125\, \texttt{x1}.

  • Then, make a scatter plot of mb-mag versus color. Add the uncertainties and fit the plot by a line: mB∗−mag ≡ β colorm_B^*-\texttt{mag} \,\equiv\, \beta\, \texttt{color}. Print the equation of the fit on the plot and comment it.
#### To complete
fit,cov = np.polyfit(   x=df['color'],y=delta,deg=1,    cov=True,w=1/df['dcolor'])
beta =            fit[0]
beta_err =        np.sqrt(cov[0,0])
####

line_beta = np.polyval(fit, df['color'])
print('Beta value: ',beta,' +/- ',beta_err)
Beta value:  2.7342201610653505  +/-  0.08755128241575162

fig = plt.figure()
plt.errorbar(x=df['color'], y=delta, xerr=df['dcolor'], yerr=df['dmb'], fmt='.', color='b', markersize=1, alpha=0.1)
plt.plot(df['color'], line_beta, 'r-',lw=2)
plt.xlabel('$\mathtt{color}$',size='14')
plt.ylabel('$m^{*}_{B}(z) - m^{*}_{B,\mathrm{model}}$ [mag]',size='14')
plt.grid()
plt.show()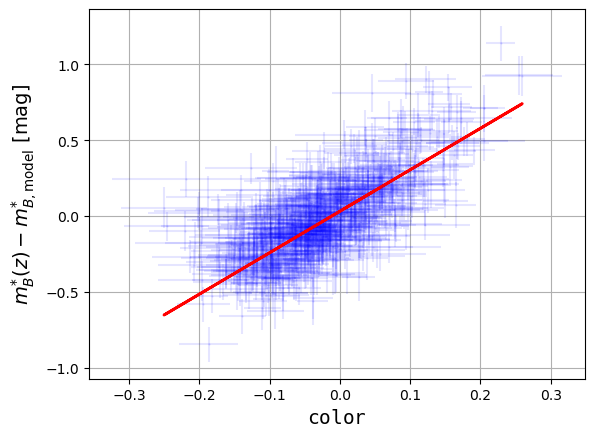
<Figure size 640x480 with 1 Axes>

We see a systematic trend between the data points: it means that the supernovae are not so standard and that their magnitude depends on un-modelled physical properties. The fit gives mB∗−mag≈−2.5 colorm_B^*-\texttt{mag} \approx -2.5 \,\texttt{color} (the brighter-bluer rule).

  • Propose a way to correct the measured magnitudes in order to remove the systematic trends that we observed. Fill the array mb_corr with your proposition.
#### To complete
mb_corr = df['mb'] - alpha*df['x1'] - beta*df['color']
mb_corr_err = np.sqrt(df['dmb']**2+(alpha*df['dx1'])**2+(beta*df['dcolor'])**2)
####
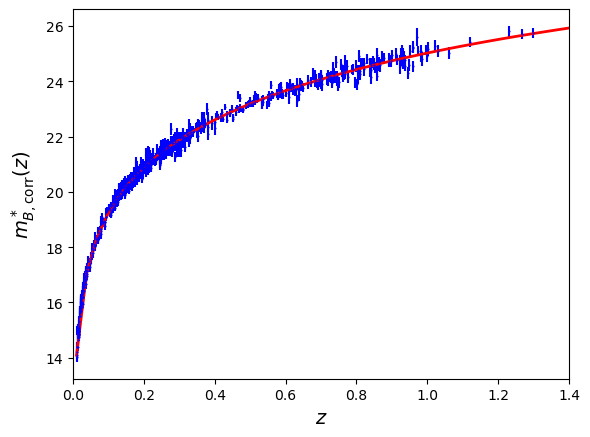
  • Make a new Hubble diagram using these corrected magnitudes and superimpose your cosmological model. Fill the delta_corr and chisq_corr arrays propagating all the uncertainties, as well as the RMS_corr and total_chisq_corr variables as previously for this new fit. Comment.
#### To complete
fig = plt.figure()
ax = fig.add_subplot(111)
plt.errorbar(x=df['zcmb'], y=mb_corr,xerr=np.abs(df['dz']),yerr=mb_corr_err,fmt='.',color='b',markersize=1)
plt.plot(z, mu_f(z, 0.3, 0.7, M),'r-',lw=2)
ax.set_xlabel('$z$',size='14')
ax.set_xlim([0.000,1.4])
#ax.set_ylim([-1.6,1.1])
ax.set_ylabel('$m^*_{B,\mathrm{corr}}(z)$',size='14')
#ax.set_xscale('log')
plt.show()
####
<Figure size 640x480 with 1 Axes>
pval, pcov = curve_fit(mu_f, df['zcmb'], mb_corr, sigma=mb_corr_err, p0=(0.3,0.7,24), absolute_sigma=True)
print(pval)
[ 0.2516525   0.63296623 24.0802872 ]

#### To complete
delta_corr = mb_corr - mu_f(df['zcmb'], *pval)
chisq_corr = delta_corr**2/mb_corr_err**2

# Fit control table
RMS_corr =                 np.std(delta_corr)
total_chisq_corr =         np.sum(chisq_corr)
####

print('Corrected RMS: ',RMS_corr)
print('Corrected total chisq: ',total_chisq_corr)
Corrected RMS:  0.1611403773821789
Corrected total chisq:  663.2587544345173

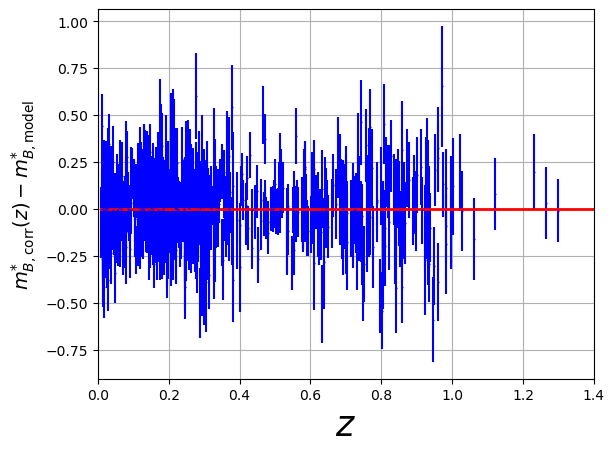
fig = plt.figure()
plt.errorbar(x=df["zcmb"], y=delta_corr, xerr=np.abs(df['dz']), yerr=mb_corr_err, fmt='.', color='b', markersize=1)
plt.plot(z,np.zeros_like(z),'r-',lw=2)
plt.xlabel('$z$',size='25')
plt.xlim([0.000,1.4])
plt.ylabel('$m^{*}_{B,\mathrm{corr}}(z) - m^{*}_{B,\mathrm{model}}$',size='14')
plt.grid()
plt.show()
<Figure size 640x480 with 1 Axes>
Lectures
CMB Degrees Of Freedom
Lectures
Thermal history