1Cosmological principle¶
Figure 1:Galaxy distribution compiled by the eBOSS survey. Every dot in this “pie” diagram is a galaxy, color coded by type: green for nearby galaxies, magenta and red for old red galaxies, blue for young blue galaxies, yellow and white for quasars. Credit: A. Raichoor (EPFL) / A. Ross (Ohio State Univ.) / SDSS Collaboration
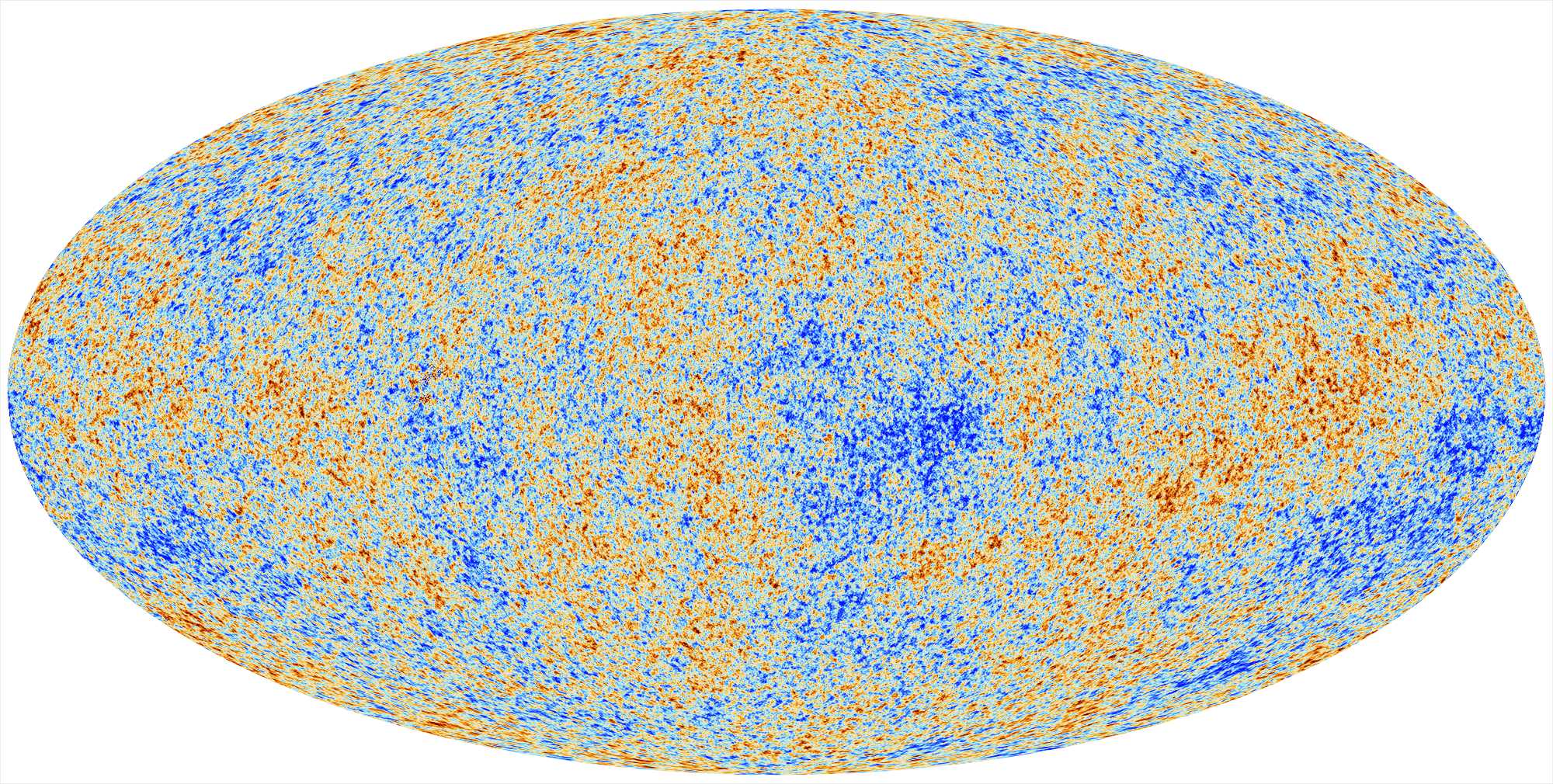
Figure 2:Temperature map of the Cosmic Microwave Background (CMB) observed by the Planck satellite. The relative difference observed between the temperature of hot (red) and cold (blue) spots relative to the mean is of the order of .
To be able to build a model of the Universe, i.e. a theoretical construct capable of describing the contents of the Universe and its evolution, we need to solve Einstein’s equation of General Relativity. But to what level of detail is it necessary to describe the Universe sufficiently well on large scales? Parametrizing Einstein’s equation to include the scale of the solar system is both illusory and unnecessary. What is the structure of the Universe on the largest scales? Here, nature has given us a wonderful gift, which will considerably simplify the writing of a cosmological model based on the equations of General Relativity.
the Universe is homogeneous: the metric therefore does not depend on an observer’s position in space, so no position is particular in the Universe. This assertion, based on the Copernican principle, is only statistically true, as we can observe that matter has formed lumps (planets, stars, galaxies, etc.) in the middle of large voids. However, observation of the Universe on large scales shows that the Universe is indeed globally homogeneous on scales larger than Mpc[1] (see Figure 1 and for example Scrimgeour et al. (2012) for a measure of the Universe’s homogeneity by counting galaxies).
the Universe is isotropic: no direction is privileged. This means that observations made in two different directions across the sky are equivalent. This is well verified by observations of the cosmic microwave background (CMB), whose temperature is measured to be identical at K in all directions of space Mather et al., 1999. Only temperature fluctuations of the order of K are detected in this image of the young Universe (see Figure 2 and for example The Planck Collaboration (2013) for a verification of the isotropy principle using the Sunyaev-Zeldovich effect).
Completely ignoring what happens at “insufficiently” large scales is the first step towards building a cosmological solution to General Relativity. Armed with these observational facts, we will impose homogeneity and isotropy on the metric and distribution of matter (i.e. the energy-impulsion tensor).
About the homogeneity of the Universe
Before presenting this cosmological solution, it’s worth asking why the cosmological principle should apply. While gravity, the dominant force shaping the large-scale structures of the universe, tends to destroy homogeneity (a slightly over-dense region in a homogeneous universe will attract matter and become increasingly over-dense), it takes longer for matter at large scales to form lumps. Since large scales appear to be more homogeneous in observations, we can assume that the universe was much more homogeneous in the past at all scales, and is becoming less so under the action of gravity. But why was it originally homogeneous? One logical answer is that an interaction other than gravity contributed to it (as, for example, pressure in a perfect gas). However, General Relativity stipulates that no interaction can propagate faster than the speed of light. We’ll see that in a theory where the evolution of the universe stems from an initial Big Bang, this creates a potential difficulty: homogenization should only be possible up to scales equal to the distance traveled by a photon between the Big Bang and today.
2Universe of maximum symmetry¶
Given the cosmological principle, we seek to determine the form that the metric of a Universe of maximum symmetry must take, i.e. a Universe whose properties are invariant by rotation and translation Weinberg, 1972[p. 379].
Metric of an isotropic Universe¶
The space-time diagram of a homogeneous, isotropic Universe has a time axis orthogonal to the spatial base vectors, due to the isotropy of the Universe. Each hypersurface at time is then a Universe of homogeneous density.
First of all, if the Universe is isotropic, we can check that the crossed components and are zero. If this were not the case, we would have a privileged direction in the universe. We can convince ourselves of this by noticing that these components are non-zero if we perform a Lorentz transformation (9)-(10), precisely when we take a frame of reference in uniform translation with respect to another, thus moving in a chosen direction.
Another way of convincing ourselves is to consider a 2D spacetime. If the metric has the form :
then the equation for light-like trajectories is :
We can then check, by solving the second-degree equation in that if , two opposite give two different values of positive . In other words, an observer will receive at different times the light pulses emitted simultaneously by two sources located at the same distance in opposite directions. This obviously breaks isotropy. The and terms of the metric are therefore zero. This means that the time vector is orthogonal to the spatial basis vectors .
What’s more, if the Universe is homogeneous, then the component can only depend on time , so that clocks do not depend on position in space. So Weinberg, 1972[p. 403]. If we call the parameter time, we see that we have a universal time at every point in space, called cosmological time. Since the Universe is homogeneous, this means that each date can be associated with a density of matter or energy that is identical for all observers, so that with a densimeter we can construct a clock common to all observers present in the Universe.
Combining the two previous results, the space-time interval can be written in the following form:
where is an elementary space vector. It is then possible to set to -1, even if it means redefining the variable time[2]. The metric thus takes the form :
where is the spatial metric, which can depend on time and position, and has 6 independent unknown components (a metric is a symmetrical tensor).
Geometry of a maximally symmetrical Universe¶
Now let’s find an explicit form for . A maximally symmetrical Universe (homogeneous and isotropic) must have the same curvature at all points in space and in all directions. This is fairly intuitive, but can also be demonstrated in General Relativity Weinberg, 1972 [p. 381]. Let be the associated radius of curvature, and let be a position vector in 3D space:
First of all, if this space has zero curvature, then the elementary distance is simply written :
Now let’s work on the case where the curvature is non-zero. To describe the curvature of a surface with the usual geometric notions, let’s study it in a space with an extra dimension. Let’s place this non-Euclidean (curved) 3D space in a 4D space of metric with Cartesian coordinates . Let be the Euclidean distance in the 3D subspace. According to the wiki:Killing–Hopf_theorem, we then have two possible 3D hyper-surfaces, of constant Gaussian curvature (see Baumann (2022), Weinberg (1972)[p. 385] and #Manifolds with constant sectional curvature) :
a 3-sphere of radius if immersed in a 4D Euclidean space:
a 3-hyperboloid of curvature if it is immersed in a 4D Lorentzian space:
2D spherical space of radius represented in a 3D Euclidean space . At a coordinate , we wish to express the length of an elementary vector tangent to the sphere in both spaces.
The last two cases of strictly positive or negative curvature are therefore defined by the constraint equation :
where here we allow the radius to depend on time, since a priori can depend on time.
Notion of curvature
If you’re confused by this reasoning, remember that it’s like describing the curvature of a circle of radius . A circle is a one-dimensional object, as there is only one direction of motion on it (parametrized by an angle , for example). But it can also be described in a 2D plane, with two coordinates and linked by the equation :
The two coordinates are linked by an equation that constrains them, so we indeed have only one degree of freedom in the end.
Similarly, a sphere (a two-dimensional object) can be studied in a space with a third dimension, i.e. three coordinates linked by the equation:
The notion of curvature can be calculated either intrinsically or using an additional dimension. Intrinsically, a living being on a circle can measure its curvature by measuring the distance covered during one revolution: it will deduce that the curvature of its circle is with deduced from the perimeter covered . If he’s able to leave the circle and travel in a second dimension, he’ll be able to observe his circle from the outside and measure the curvature of his Universe too.
The infinitesimal distance between two points of the hypersurface defined in curved 3D space of metric must be identical to that measured in 4D space, so :
where the case corresponds to spherical geometry, the case to hyperbolic geometry Weinberg, 1972 [p. 390-391].
We now need to eliminate the 4th dimension using the constraint equation to recover a 3-dimensional parameterization.
Differentiating equation (9) gives the relation
Now, the constraint equation (9) links and , so we can replace by an expression that is a function of and (i.e. without the fourth dimension):
The infinitesimal distance between 2 points in non-Euclidean 3D space of constant non-zero curvature is then :
At this stage, we can now combine the result obtained for the two non-zero curvatures with the Euclidean case by introducing the curvature parameter :
We thus have, for the three possible geometries of a maximally symmetrical Universe :
where in the case of a flat space we’d have .
Finally, let’s introduce the rescaled variable , and we get a new expression:
The Friedmann-Lemaître-Robertson-Walker metric describing a homogeneous, isotropic Universe is finally written :
The Friedmann-Lemaître-Robertson-Walker (FLRW) metric is the basic framework of the Standard Cosmological Model. The assumptions of homogeneity and isotropy led directly to a metric describing a universe with only three possible geometries (flat, 3-sphere, 3-hyperboloid) and a scaling factor affecting distances. Note that, thanks to the imposition of homogeneity and isotropy symmetries, we have reduced the writing of the metric (which is a symmetric tensor) consisting a priori of 10 unknown independent components to a tensor with a single unknown function .
It’s important to understand the physical significance of the expansion factor . First of all, according to equation (17), this factor relates the physical distance and the coordinate distance by . A particle with fixed spatial coordinates will see its physical distance from an observer in increase (or decrease) with time. This variation in distance is achieved at apparent speed:
because if the galaxy has no proper motion[3], with the point expressing a derivative with respect to time . We thus obtain a direct relationship between distance from a central observer and apparent velocity: this is Hubble’s law. The recession rate is given by the Hubble parameter, which quantifies the rate of change of the scale factor:
For a spherical universe, the scale factor also represents its radius of curvature. A dynamic spherical universe therefore corresponds to a universe with a time-varying radius of curvature. A flat space has no characteristic scale, so the value of is not a physical observable. The physically meaningful quantity for such a universe is the Hubble parameter .
To simplify notation, the time dependence of the parameters is not always made explicit, so . Parameters evaluated at the present time are designated by the subscript or exponent 0, so that . In the following, we’ll work in the system where isn’t fixed at 1.
Table 1:Representation of the two-dimensional equivalents of the three solution spaces of cosmological principles: the 2-sphere, the plane, the 2-hyperboloid.
 |  |  |
3Comoving coordinates¶
It’s important to note that not all observers see the Universe as isotropic, but only so-called comoving observers, who are locally at rest with most of the matter in their vicinity. We, for example, are not comoving observers: when we observe the temperature of the CMB, the first feature we see is a large temperature dipole (warmer on one side, colder on the opposite side), which is the result of the proper motion of our solar system in the galaxy, and of our galaxy in the Universe (and of our group of galaxies). If we were to subtract this proper motion relative to the CMB frame of reference, then we would be comoving observers. Thus, we can define a coordinate system associated with observers without proper motions, whose relative proper distances increase only with the scale factor Weinberg, 1972[p. 409].
In the FLRW metric, where the expansion of the Universe is factorized by a scale factor , the spatial coordinates are called comoving coordinates. There is considerable freedom in the choice of comoving coordinates.
Spherical parameterization¶
We often prefer the spherical parameterization with the observer (ourselves) at the origin, such as :
After some simple but lengthy calculations (see notebook and here), in all three cases of curvature the FLRW metric is written :
Curvature and finitude of the Universe
For the 3-sphere, 3-hyperboloid and the plane, the curvature of these surfaces is Weinberg, 1972[p. 412]:
The 3-hyperboloid and the plane have infinite extension. On the other hand, the 3-sphere has finite extension, but remains unbounded: a particle will never encounter an edge but a volume can be defined:
and a perimeter (length of a meridian):
Cartesian parameterization¶
The flat-universe case greatly simplifies the calculations that follow. Since the assumption of zero curvature is compatible with the increasingly stringent constraints of cosmological observations, we will henceforth concentrate our analytical developments on the flat universe, mentioning results for the general case where necessary. In the case of zero curvature, it may be convenient to use Cartesian comoving coordinates , such as :
The FLRW metric is written in a flat universe:
4Geodesics in FLRW metric¶
What is the trajectory of a free-falling particle in an FLRW metric? From General Relativity, we know that such a particle moves along a geodesic whose equation is as follows:
where is any parameter describing the position along the geodesic (e.g. proper time). Another form of the geodesic equation will help us here, obtained from the definition of the covariant derivative (31):
Let’s define the dimensionless[4] four-velocity tangent to the trajectory by . Then :
Demonstration
The preceding equality is demonstrated in Hobson et al. (2006)[p. 81]. Here is the gist of it:
because the metric is a symmetrical tensor so .
From this form of the geodesic equation (see Hobson et al., 2006[p. 81] for a demonstration), let’s calculate the form that the contravariant vector must take in a FLRW metric for a particle in free fall.
Let’s start with the case and use the spherical coordinates . Since the FLRW metric does not depend on , then :
so is a motion constant. Furthermore:
whose expression cancels at the origin at , where we observe. Since the component is constant, it is identically zero along the trajectory. We deduce:
.
Let’s move on to the case. The only component of the metric depending on is but is identically zero, so :
In the same way, we also have :
which cancels out at , so is zero all along the trajectory. From this we deduce:
5Spectral shift, or redshift¶
Figure 6:Notations for calculating redshift and cosmological distances in comoving coordinates.
To measure the expansion history of the Universe, we need access to the scale parameter . This is made possible by measuring the spectral shift of light coming from distant sources. In the FLRW metric, let’s place ourselves by convention at the center (), and consider an object located at comoving coordinates , emitting a photon at time (see Figure 6). For this photon, traveling at the speed of light, in the FLRW metric we have, at any instant:
because along its geodesic and are constant (). Let’s assume is the instant of reception of this wave at . Then, thanks to the previous equation, we have the relation :
with the minus sign coming from the fact that we consider a photon going from the source towards the observer at 0.
For an electromagnetic wave with period , the expression (38) being valid at any instant, we can calculate the same integral for the wave emitted at instant and received at instant (we assume that the period will vary with time):
Equating the expressions (39) and (40), since the period is small compared to the variations in the scale factor for usual electromagnetic waves, we obtain:
Directly, if space is expanding, then and the received wavelength is therefore greater than the transmitted wavelength . We then define the spectral shift, commonly called redshift due to the fact that almost all observed galaxy spectra are redshifted, as :
The spectral shift is both directly related to the scale parameter , and to an experimental quantity that can be directly measured on the emission spectrum of distant objects. Indeed, by looking at the position of the absorption and emission lines of distant objects, we can deduce their spectral shifts relative to the same chemical elements located on Earth, at rest. This experimental data is therefore often associated with the definition of distances in cosmology. The most distant galaxy observed to date has a redshift (JWST: Carniani et al. (2024)).
Solution to Exercise 1
Tired light theory and time dilation
Tired light is a hypothesis proposed to explain the Hubble-Lemaître law without invoking an expansion of the Universe, introduced by Fritz Zwicky in 1929 as a possible alternative explanation. Tired light models invoke a progressive loss of energy of photons as they traverse the cosmos to produce the redshift-distance law. This poses three main problems.
There is no known interaction capable of degrading the energy of a photon without also modifying its momentum, which would lead to a blurring of distant objects, which is not observed.
The tired light model does not predict the observed time dilation of supernova light curves at large redshift. This time dilation is a consequence of the standard interpretation of redshift: a supernova that takes 20 days to decay will appear to take 40 days to decay when observed at redshift (Figure 7).

Figure 7:Stretch factor of Type Ia supernovae (i.e. duration normalized to 1 today) as a function of . Cosmological time dilation requires that this varies as whereas the tired light hypothesis predicts no time dilation. Sources: notebook SNIa duration and time dilation and Goldhaber et al., 2001.
We also observe that the supernova explosion rate evolves as , another sign of time dilation.
If light reddens without being diluted by expansion, then an initial blackbody spectrum evolves into a spectrum that deviates from the blackbody assumption. Indeed, Planck’s law (wiki:Planck’s_law) combines a density of vibrational modes with a prefactor and the Bose-Einstein distribution containing an exponential . If light gets tired, only the exponential is affected because the number of modes does not change with redshift if there is no expansion. The prefactor then differs by a shift of compared to a Planck law undergoing the expansion of the Universe. However, we observe that the cosmic microwave background follows the blackbody radiation law extremely precisely Mather et al., 1999.
6Proper distance and comoving distance¶
Proper distance defines the physical distance between two objects at a time . Let a transmitting object be located at comoving coordinates . By definition, the proper distance between this object and an observer located at the origin is along a curve at constant and and is equal to :
where is the comoving distance between this object and the observer:
We can see that the proper distance has the unit of a length, whereas the comoving distance is dimensionless. The latter represents distance in coordinate space and is independent of the expansion of the Universe. The proper distance, on the other hand, evolves over time with the scale factor.
Reciprocally, we define as follows:
Now let’s imagine that this distance can be perceived through the journey of a photon. Light travels along a geodesic, so in the FLRW metric we have and :
Therefore:
with the photon traveling along the direction for . The comoving distance is rewritten as
Let’s express this distance in terms of the redshift , which, as we all know, is an experimental observable. Integrals can be transformed between the variables , by defining the expansion rate , and between the variables and by defining the redshift:
Hence the comoving distance in terms of time , scale factor and redshift :
Table Table 3 summarizes how the parameters , and are converted at different times in the chronology of the Universe.
Table 3:Conversion of parameters , and . Note , the age of the Universe today.
| a | t | z | |
|---|---|---|---|
| reception (today) | 0 | ||
| emission (past) | |||
| beginning of the Universe | 0 | 0 | |
| end of time | -1 |
The proper distance is the distance that could actually be measured between two objects at time . If we choose an object located at the comoving coordinate and a comoving observer in 0, then the proper distance today at is simply written for the three curvature cases:
and is expressed in units of length. The notion of proper distance is illustrated Figure 8.
Figure 8:Proper distance between the Earth and a distant galaxy with no apparent proper velocity. (a) Today, the measured distance between the Earth and this galaxy is light-years in flat space. (b) At another date , this distance evolves to . (c) Proper distance in spherical space.
Solution to Exercise 2 #
The comoving coordinate is explicitly the polar angle between the observer and the galaxy. The proper distance is the arc length, which is as in usual geometry. The coordinate is related to the angle by :
with the radius of the circle of colatitude .
Using polar projection Figure 9, we see that is the angle delimiting an arc of size and radius , the radius of ’s latitude circle. Thus :
Thanks to the parameterization , we can see that this equality works in both flat and curved space.
If we prefer to reason mathematically rather than graphically, using the FLRW metric, we can also demonstrate :
So again we get .
It’s easy to check that we have the same expressions in the flat case, and we’ll admit them in hyperbolic geometry. The coordinate is therefore useful for making calculations and drawings in the flat case and translating these results into the curved case (which isn’t so easy with ).
Figure 9:Geometry in a spherical universe.
7Cosmic time and conformal time¶
Time deserves a special mention. In our ideal Universe, with no over- or under-densities of matter, all clocks that follow expansion (i.e. with no proper motion of their own) beat the second at the same rate. With infinite time at our disposal to set all the clocks in the Universe, we can propose a universal convention for synchronizing our clocks. For example, when the temperature of the CMB reaches a given value, all the civilizations in the Universe can decide that this corresponds to a certain date. It is therefore possible to define a cosmic time, common to all comoving observers Weinberg, 1972 [p. 409].
1 parsec (pc) light-years m. light-years.
We can introduce a new time variable such that .
The term is called peculiar velocity. Galaxies have a peculiar velocity of the order of km/s, which adds to the expansion effect. This is dominant in the local Universe up to Mpc, equivalent to .
For a massive particle, we can write that .
- Scrimgeour, M. I., Davis, T., Blake, C., James, J. B., Poole, G. B., Staveley-Smith, L., Brough, S., Colless, M., Contreras, C., Couch, W., Croom, S., Croton, D., Drinkwater, M. J., Forster, K., Gilbank, D., Gladders, M., Glazebrook, K., Jelliffe, B., Jurek, R. J., … Yee, H. K. C. (2012). The WiggleZ Dark Energy Survey: the transition to large-scale cosmic homogeneity. Monthly Notices of the Royal Astronomical Society, 425(1), 116–134. 10.1111/j.1365-2966.2012.21402.x
- Mather, J. C., Fixsen, D. J., Shafer, R. A., Mosier, C., & Wilkinson, D. T. (1999). Calibrator Design for the COBE Far-Infrared Absolute Spectrophotometer (FIRAS). The Astrophysical Journal, 512(2), 511–520. 10.1086/306805
- The Planck Collaboration. (2013). Planck intermediate results. XIII. Constraints on peculiar velocities. Astronomy & Astrophysics, 561, A97. 10.1051/0004-6361/201321299
- Weinberg, S. (1972). Gravitation and cosmology: principles and applications of the general theory of relativity. http://www.lavoisier.fr/livre/notice.asp?ouvrage=1382255
- Baumann, D. (2022). Cosmology. Cambridge University Press. https://cmb.wintherscoming.no/pdfs/baumann.pdf
- Einstein, A., & Straus, E. G. (1945). The Influence of the Expansion of Space on the Gravitation Fields Surrounding the Individual Stars. Rev. Mod. Phys., 17(2–3), 120–124. 10.1103/RevModPhys.17.120
- Mars, M., Mena, F. C., & Vera, R. (2013). Review on exact and perturbative deformations of the Einstein–Straus model: uniqueness and rigidity results. General Relativity and Gravitation, 45(11), 2143–2173. 10.1007/s10714-013-1574-1
- Günther, T. (2013). Matching of local and global geometry in our universe [Phdthesis]. 10.13140/2.1.4972.5442
- Schücking, E. (1954). Das Schwarzschildsche Linienelement und die Expansion des Weltalls. Zeitschrift Fur Physik, 137(5), 595–603. 10.1007/BF01375011
- Carrera, M., & Giulini, D. (2010). Influence of global cosmological expansion on local dynamics and kinematics. Reviews of Modern Physics, 82(1), 169–208. 10.1103/revmodphys.82.169
- Hobson, M. P., Efstathiou, G. P., & Lasenby, A. N. (2006). General Relativity: An Introduction for Physicists. Cambridge University Press. https://books.google.fr/books?id=5dryXCWR7EIC
- Carniani, S., Hainline, K., D’Eugenio, F., Eisenstein, D. J., Jakobsen, P., Witstok, J., Johnson, B. D., Chevallard, J., Maiolino, R., Helton, J. M., Willott, C., Robertson, B., Alberts, S., Arribas, S., Baker, W. M., Bhatawdekar, R., Boyett, K., Bunker, A. J., Cameron, A. J., … Willmer, C. N. A. (2024). Spectroscopic confirmation of two luminous galaxies at a redshift of 14. Nature, 633(8029), 318–322. 10.1038/s41586-024-07860-9
- Goldhaber, G., Groom, D. E., Kim, A., Aldering, G., Astier, P., Conley, A., Deustua, S. E., Ellis, R., Fabbro, S., Fruchter, A. S., Goobar, A., Hook, I., Irwin, M., Kim, M., Knop, R. A., Lidman, C., McMahon, R., Nugent, P. E., Pain, R., … York, T. (2001). Timescale Stretch Parameterization of Type Ia Supernova B-Band Light Curves. The Astrophysical Journal, 558(1), 359. 10.1086/322460