Jusqu’à présent, nous avons étudié l’évolution d’un Univers homogène, au moins aux très grandes échelles, au-delà d’environ . Or, aujourd’hui on observe que la matière est agglomérée sous forme de planètes, étoiles, galaxies, amas de galaxies et super-amas de galaxies. La question qui se pose alors dans ce chapitre est : comment se forment ces structures dans un Univers en expansion ? Si la formation des astres les plus petits implique beaucoup de processus physiques et est très dépendante des conditions initiales locales, il est possible d’élaborer un modèle linéaire simple de l’évolution des structures les plus grandes , comme les amas ou super-amas de galaxies. Pour ce faire, nous allons simplement utiliser une théorie newtonienne des perturbations linéaires, et calculer l’évolution de ces perturbations dans un Univers en expansion.
Figure 1:Échelles de taille et de masse dans l’Univers.
1Régime de validité¶
Toutefois, énonçons les conditions nécessaires à la validité de la théorie newtonienne des perturbations. Une première condition évidente est que la perturbation de la métrique et du tenseur énergie-impulsion doit être faible. Dans le cas de la matière non relativiste, cela signifie que les perturbations de la densité doivent rester faibles devant la densité moyenne i.e. . Les perturbations du champ de gravité sont également faibles devant le champ gravitationnel moyen i.e. .
Mais pour pouvoir revenir à la gravité newtonienne dans un espace-temps homogène en expansion et n’étudier que les perturbations de la densité, il y a une autre condition. La taille des régions étudiées doit être beaucoup plus petite que le rayon de Hubble , car en gravitation newtonienne l’interaction se propage instantanément. Si la structure est de taille cosmologique, le temps que l’information d’une région en effondrement ait voyagé jusqu’à ses frontières, le facteur d’expansion change de manière significative : une situation qui ne peut évidemment pas être traitée en utilisant la gravité newtonienne. On ne considère donc que les structures de taille très inférieure à pour pouvoir supposer que la force gravitationnelle se propage instantanément dans la structure vis à vis du taux d’expansion de l’Univers.
2Préambule d’acoustique classique¶
Le champ de matière non-relativiste est décrit par un modèle de fluide parfait. Regarder l’évolution de perturbations dans un fluide parfait, c’est s’intéresser au domaine de l’acoustique. Rappelons-en ici quelques notions utiles.
Dans une description eulérienne des fluides, pour un fluide parfait au repos, on définit son champ de vitesse , son champ de pression et son champ de densité massique comme constants :
Par dessus, on superpose des perturbations de faible amplitude :
Les surpressions engendrées changent l’énergie interne des perturbations et donc leur température, et ce travail des forces de pression permet la propagation de l’énergie acoustique. En acoustique, on mesure que les compressions sont adiabatiques et réversibles, c’est-à-dire que la taille des perturbations est supérieure au libre parcours moyen des particules du fluide: on peut alors négliger la conduction de chaleur. On utilise donc la compressibilité isentropique au lieu de la compressibilité isotherme :
On en déduit le lien entre perturbations de pression et de densité via la compressibilité isentropique :
On a également conservation locale de la masse :
Comme le fluide est parfait, sa dynamique est régi par l’équation d’Euler (Navier-Stokes sans viscosité) :
où usuellement on néglige la gravitation. En combinant ces trois équations, on obtient une équation de d’Alembert :
avec la célérité du son.
Pour un gaz parfait et des transformations isentropiques, on utilise la Loi de Laplace avec le rapport des capacités calorifiques à pression et volume constants, aussi appelé l’indice adiabatique. Si les particules du fluide possèdent degrés de liberté (translations, rotations, vibrations) pour stocker de l’énergie sous forme cinétique (thermique), alors l’indice adiabatique vaut . Pour un gaz diatomique comme l’air à température usuelle, il y a degrés de liberté (3 translations et 2 rotations) donc . On en déduit une formule pour la célérité du son fonction de la température et de la masse des particules[1] :
avec la masse molaire du fluide et la masse effective d’une particule d’air si c’est le milieu considéré, calculée par :
3Acoustique dans un espace en expansion avec gravitation¶
A l’émission du CMB, on constate que l’Univers est un gaz parfait de matière non-relativiste, légèrement inhomogène, avec des surdensités de taille réduite (de l’ordre de ). Ces fluctuations vont a priori s’accentuer au cours du temps grâce à l’attraction gravitationnelle, pour aboutir à un Univers où le contraste de densité est de l’ordre de [2] ( Figure 1,Figure 2). Quels sont les mécanismes permettant cette croissance?
La formation des grandes structures de l’Univers peut être appréhendée par une théorie linéaire des perturbations dans le fluide parfait constitué par la matière non-relativiste après la recombinaison. Pour étudier l’évolution de ces perturbations de densité dans le champ de matière, il s’agit donc de réécrire les équations de l’acoustique précédentes, dans le contexte particulier d’un milieu en expansion et soumis aux lois de la gravité.

Figure 2:An artistic celebration of the Dark Energy Spectroscopic Instrument (DESI) Year 1 data, showing a slice of the larger 3D map that DESI is constructing during its five-year survey. DESI is mounted on the Nicholas U. Mayall 4-meter Telescope at Kitt Peak National Observatory. Credit: DESI Collaboration/KPNO/NOIRLab/NSF/AURA/P. Horálek/R. Proctor
Figure 3:Cette simulation montre comment la gravité affecte la position des galaxies observées, modifiant ainsi la façon dont la matière s’agglomère pour former les structures cosmiques. Comme différents modèles de gravité prédisent différentes formations des structures, les scientifiques de DESI peuvent comparer les observations avec les prédictions et ainsi tester la gravité aux échelles cosmiques. Credit: Claire Lamman et Michael Rashkovetskyi / DESI collaboration
Systèmes de coordonnées¶
Les équations de la physique classique sont valables en utilisant des quantités physiques (non comobiles) : distance propre, temps propre, etc... L’utilisation des distances physiques comme système de coordonnées est cependant peu pratique dans un Univers en expansion car temps et distance sont liés. Une méthode plus pratique consiste à écrire ces équations dans l’espace comobile. Notons :
le vecteur position physique (dont la norme est la distance propre ),
le vecteur position comobile (dont la norme est la distance comobile ),
la vitesse physique,
la vitesse comobile.
Nous avons les relations suivantes :
Bien que le flot de Hubble (premier terme de (11)) ne doit pas être considéré comme une vitesse réelle, il apparaît dans la relation entre et . Cela poserait un problème si elle pouvait prendre des valeurs de l’ordre de (ou plus grandes). Mais la condition selon laquelle garantit que (voir section Section 1).
Comment passer du système de coordonnées physiques au système de coordonnées comobiles ? La conversion des dérivées partielles spatiales est assez simple :
La dérivée partielle temporelle nécessite un examen plus attentif. Écrivons la différentielle d’une fonction du temps et de l’espace quelconque :
Donc par identification :
Conservation de la masse¶
Dans l’espace physique, l’équation de continuité s’écrit :
En utilisant la densité comobile , nous pouvons exprimer cette équation dans l’espace comobile :
En introduisant la formule classique du calcul vectoriel
où est un scalaire et un vecteur, l’équation ci-dessus se réduit à :
L’équation de continuité prend donc exactement la même forme dans l’espace comobile, en utilisant des variables comobiles. Ce n’est toutefois pas le cas si l’on utilise la vitesse particulière .
Équation d’Euler¶
Dans l’espace physique, l’équation d’Euler pour un fluide parfait (non visqueux) autogravitant prend la forme habituelle :
Dans l’espace comobile, elle se transforme en :
avec le potentiel comobile. En veillant à ce que :
l’équation d’Euler en coordonnées comobiles se réduit à :
Nous pouvons voir deux termes supplémentaires par rapport à la version de l’équation d’Euler écrite en coordonnées physiques. Le terme supplémentaire est une force de traînée créée par l’expansion sur les vitesses comobiles. Le dernier terme ne dépend que de quantités cinématiques, c’est donc une force fictive liée au changement de système de coordonnées, non nulle si et seulement si il n’y a pas d’accélération entre les référentiels (). Dans un univers en expansion accélérée (), il correspond à une force fictive centripète.
Equation de Poisson¶
Dans un univers sans constante cosmologique, de la relativité générale on en déduit l’équation de Poisson habituelle dans la limite des champs faibles (38) :
où est le potentiel gravitationnel. Compte tenu de la relation entre le potentiel et la force newtonienne, le potentiel comobile est naturellement défini comme , et l’équation de Poisson est également inchangée dans l’espace comobile :
4Théorie newtonienne des perturbations¶
Solution d’ordre 0¶
Dans un univers homogène et isotrope, à l’ordre 0 la densité massique ne dépend pas de l’espace et la matière est globalement au repos. Il n’y a donc pas de vitesse particulière globale et l’équation de conservation de la masse dans l’espace comobile (18) admet la solution d’ordre 0 :
La densité massique comobile reste donc stationnaire et homogène. L’intégration de l’équation de Poisson (24) en coordonnées sphériques[3] donne :
Si on utilise les équations de Friedmann (60) :
pour un Univers dominé par la matière avec et , on obtient la force dérivée du potentiel gravitationnel :
Le gradient du champ gravitationnel donne à l’ordre 0 une force centrifuge reflétant le caractère répulsif de l’expansion de l’univers.
A partir de l’équation d’Euler (22) et des résultats précédents, on aboutit logiquement à retrouver que donc :
consistante avec un Univers homogène.
Solution linéaire d’ordre 1¶
Considérons de petites perturbations autour de la solution d’ordre zéro :
La quantité est appelée contraste de densité et est très utilisée dans la théorie de la formation des structures. Notons qu’elle a la même valeur dans l’espace physique et dans l’espace comobile. En injectant ces expressions dans les équations de continuité, de Poisson et d’Euler, la solution d’ordre zéro disparait (comme prévu) et en supprimant les termes d’ordre 2, nous obtenons l’ensemble d’équations linéarisées :
En prenant la divergence de l’équation d’Euler linéarisée (34), la dérivée temporelle de l’équation de conservation de la masse linéarisée (33) et en réinjectant l’équation de Poisson (35), nous obtenons finalement :
On introduit la vitesse du son dans le milieu pour des compressions adiabatiques :
Alors on obtient l’équation de croissance des perturbations dans l’espace comobile :
Comparons cette équation à l’équation de d’Alembert obtenue en acoustique classique (7). Nous avons deux termes supplémentaires :
un terme de frottement qui va ralentir la formation des structures d’autant plus que le taux d’expansion est élevé, sur des échelles de temps cosmologiques ;
un terme source proportionnel à qui modélise l’effondrement gravitationnel (plus la structure est marquée, plus elle s’effondre). L’évolution des perturbations de matière est donc dictée par les intensités relatives de la force gravitationnelle (attractive), des forces de pression (répulsives), et de l’expansion de l’Univers (amortissement).
Vitesse du son¶
Dans un Univers dominé par la radiation, les propriétés du gaz relativiste sont :
d’où la vitesse du son dans le plasma relativiste :
Juste avant la recombinaison, la propagation des ondes sonores est donc relativiste dans le plasma primordial.
Dans un Univers dominé par la matière non relativiste, les propriétés thermodynamiques des baryons sont :
avec la masse effective des baryons dans un mélange de gaz d’hydrogène atomique et d’hélium (notez la ressemblance avec (10)), et l’indice adiabatique des baryons car l’hydrogène est sous forme atomique (et l’hélium bien sûr). Pour une transformation adiabatique réversible, avec la loi de Laplace on a , la température des baryons évolue en :
Or donc la température des baryons évolue en :
Avec , pour les baryons la pression varie en et la température en . La vitesse du son dans le gaz de baryons s’écrit :
Juste après le découplage des photons et des électrons, la température des baryons est de donc la vitesse du son dans le gaz de baryons est d’environ . Autour de la recombinaison, le changement est de plusieurs ordres de grandeur donc l’évolution des perturbations change drastiquement à cet instant. Puis la température des baryons décroît en , du moins tant que le chauffage par le rayonnement interstellaire ne change la donne (autour de ). La vitesse du son décroît donc en dans notre modèle linéaire.
/Users/jneveu/miniforge3/envs/m2-cosmo/lib/python3.11/site-packages/astropy/cosmology/flrw/base.py:1072: IntegrationWarning: The integral is probably divergent, or slowly convergent.
return quad(self._lookback_time_integrand_scalar, z, inf)[0]
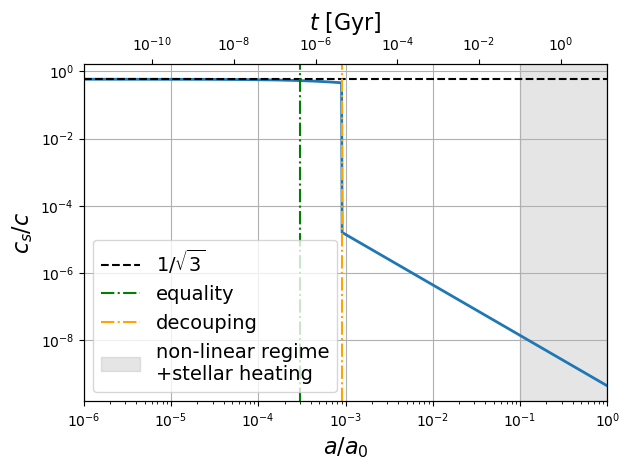
Figure 4:Vitesse du son dans l’Univers en fonction du facteur d’échelle . La légère diminution entre l’équivalence et le découplage est donnée par l’équation (48) (voir encadré). Le calcul est inexact quand on rentre dans le régime non-linéaire de la croissance des structures i.e. lorsque (région grisée). De plus, vers ce redshift également, le gaz de baryons est chauffé par le rayonnement stellaire donc la température des baryons n’évolue plus en .
Mélange de baryons et de photons couplés
Tant que les photons sont couplés aux électrons libres, ils sont mécaniquement couplés au gaz de baryons par la force de Coulomb. Pendant la période où l’Univers est dominé par la matière mais où les photons sont encore couplés aux électrons (Weinberg (1989) p.509,566) :
Instabilité de Jeans¶
Les solutions à l’équation d’évolution des perturbations (38) seront étudiées au prochain semestre, mais on peut déjà étudier leurs comportements à partir de leur relation de dispersion. Recherchons des solutions en ondes planes de la forme :
et étudions les solutions dans le domaine de Fourier. La relation de dispersion s’écrit :
En négligeant le terme d’amortissement (de l’ordre de l’âge de l’Univers) devant le temps caractéristique d’évolution des perturbations (), on aboutit à :
avec . C’est la même relation de dispersion que celle des ondes électromagnétiques dans un plasma. On définit le nombre d’onde de Jeans (The Royal Society (1902)) et la longueur de Jeans par :
Si , alors donc on a une solution oscillante i.e. une onde acoustique qui se propage : les perturbations de taille petite devant la longueur de Jeans oscillent grâce à la force de pression et ne croissent pas.
Si , donc on a une solution non oscillante en exponentielle : les grandes structures évoluent seulement sous l’effet de la gravité et s’accroissent (et les vides décroissent).
Comme l’échelle évolue avec l’expansion () ainsi que la longueur de Jeans, la discussion n’est pas aisée à mener le long de l’histoire de l’Univers. Définissons la masse dans une sphère de rayon , conservée avec l’expansion, et comparons-la à la masse de Jeans :
Nous n’avons maintenant plus qu’une quantité qui varie avec :
Si , alors la structure est trop légère et la pression peut compenser la force de gravité : la structure oscille.
Si , alors la structure est trop lourde et s’effondre gravitationnellement.
Le tracé de la masse de Jeans en fonction du facteur d’échelle permet de prédire quelles sont les structures pouvant s’effondrer gravitationnellement et celles dont la croissance est empêchée Figure 5 (Weinberg (1989) p. 565).
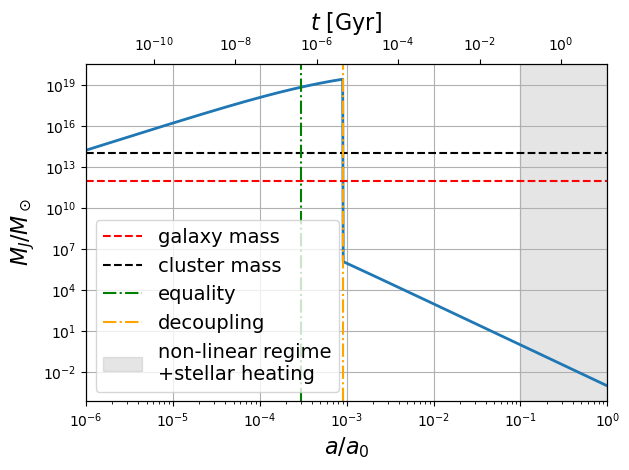
Figure 5:Evolution de la masse de Jeans en fonction du facteur d’échelle . Le calcul est inexact quand on rentre dans le régime non-linéaire de la croissance des structures i.e. lorsque (région grisée). De plus, vers ce redshift également, le gaz de baryons est chauffé par le rayonnement stellaire donc la température des baryons n’évolue plus en .
Décrire la croissance des structures avant la recombinaison contredit l’hypothèse non-relativiste sur laquelle repose notre étude. Cependant, l’échelle de la vitesse du son reste une échelle pertinente et de plus la matière non-relativiste domine après l’équivalence. Sachant cela (et que l’étude relativiste ne donne pas de résultats fondamentalement différents de ce qui suit), on va se permettre de discuter de la croissance des grandes structures dans l’Univers primordial et récent (bien qu’elle soit non-linéaire aujourd’hui).
D’après la Figure 5, on voit qu’avant le découplage des structures ayant la masse d’une galaxie ou d’un amas de galaxie ne sont pas suffisamment lourdes pour s’effondrer (ou alors juste dans les premiers instants de l’Univers). Des ondes de pression les parcourent et elles oscillent. Toutefois après le découplage, la vitesse du son chute de 5 ordres de grandeur. Le découplage des photons gèle les ondes de pression et des structures de la masse de galaxies et même de galaxies naines peuvent commencer leur croissance.
Description statistique des perturbations¶
Champ gaussien¶
Décrivons le champ dans l’espace de Fourier. Utilisons la convention suivante pour les transformées de Fourier directe et inverse :
Le champ en Fourier est un nombre complexe décrit par son module et sa phase que nous noterons :
Au moment du Big Bang, on peut penser que la phases sont distribuées de façon aléatoires et indépendantes (pas de couplage entre échelles dues à des corrélations statistiques entre modes, voir le chapitre ). Si les perturbations suivent une évolution linéaire, alors les modes évoluent indépendamment les uns des autres : les phases restent des variables aléatoires indépendantes. Or si les phases d’un champ en Fourier sont aléatoires et indépendantes, alors ce champ est appelé champ gaussien. Si on examine la transformée de Fourier inverse (55), on note que le champ dans l’espace réel est le résultat de la somme de variables aléatoires indépendantes donc on peut appliquer le théorème centrale limite : le résultat de la somme suit une distribution gaussienne. Ce champ est donc statistiquement entièrement défini par les deux paramètres de la distribution gaussienne, sa moyenne et sa variance :
avec puisque ce champ est physique donc réel (). En toute rigueur, la notation désigne une moyenne sur un ensemble statistique de réalisations. Cependant comme nous ne disposons que d’une seule réalisation d’univers, ce sera une moyenne sur un volume avec les échantillons de . La moyenne est nulle par définition du contraste de densité, intéressons-nous donc à la variance.
Spectre de puissance de la matière¶
Le conjugué d’un mode de Fourier s’écrit :
donc la variance se réécrit :
Pour un champ isotrope, seule la norme du vecteur importe donc :
On définit le spectre de puissance de la matière par :
où désigne ici la fonction delta de Dirac, homogène à l’inverse d’un volume. Au sens des distributions, sa transformée de Fourier vaut 1 ce qui permet d’en déduire une formulation sous la forme d’une intégrale:
Le spectre de puissance est donc homogène à un volume : . Pour un champ réel, les modes de Fourier conjugués vérifient donc on peut reprendre la définition du spectre de puissance et calculer la moyenne de la norme des modes de Fourier :
avec un volume d’intégration, en pratique fini car les mesures ou simulations sont discrètes et réalisées dans un volume fini. Pour un champ isotrope, on peut réaliser la moyenne d’ensemble en moyennant sur les modes de même norme . On obtient :
Le spectre de puissance de la matière à une échelle est donc la moyenne des modes de Fourier de même norme. On définit également la variance logarithmique modal comme :
C’est la contribution à la variance des modes de norme par intervalle logarithmique :
Dans le cadre d’une croissance linéaire des structures, les modes de Fourier sont indépendants. Le spectre de puissance de la matière à un redshift peut alors s’écrire :
où on définit la fonction de transfert et le spectre de puissance de la matière initial . Que peut-il valoir ? Si on fait l’hypothèse qu’au début de l’Univers les perturbations de densité sont aléatoires et qu’il n’y a aucune échelle de distance particulière, une loi de puissance est appropriée :
Pour les conditions initiales, on va préférer s’intéresser aux perturbations scalaires de la métrique . Or par l’équation de Poisson . On en déduit le spectre de puissance normalisé des fluctuations scalaires :
Au début des années 1970, les cosmologistes Harisson et Zel’dovitch proposent que toutes les échelles doivent participer également à la variance au début de l’Univers, aucune échelle spatiale ne compte plus que les autres (Harrison (1970), Zeldovich (1972)). Si cette hypothèse est vraie, alors on doit avoir .
La prédiction théorique du spectre en regardant l’évolution des différentes échelles de perturbations de densité le long de l’histoire de l’Univers est une courbe convexe, présentant une forme en aux grandes échelles (trop grandes pour avoir évoluées) et en aux petites échelles (celles qui s’effondrent). La bascule entre les deux régimes est le mode correspondant à l’échelle de l’horizon à l’équivalence (voir Figure 6).

Figure 6:Spectre de puissance de la matière mesuré par différentes techniques et comparé aux prédictions théoriques linéaires (trait plein) et non-linéaires (trait pointillé), adapté de Chabanier et al. (2019).
Fonction de corrélation et ¶
Le spectre de puissance est relié à la fonction de corrélation dans l’espace physique par les formules suivantes :
On note que l’autocorrélation redonne la variance du champ : , et que cette dernière correspond grosso modo à l’intégrale du spectre de puissance de la matière donc à sa normalisation. La mesure de la normalisation du spectre de puissance est donc une façon de mesurer l’agglomération de la matière : plus le spectre de puissance est élevée, plus la variance du champ de matière est élevé, donc plus la matière est condensée dans des surdensités. D’un point de vue expérimental, le spectre de puissance se mesure par le comptage de galaxies dans des sphères de rayon :
Aujourd’hui, Tristram, M. et al. (2024) mesure :
Comme cette valeur est proche de 1, cela signifie qu’à des échelles plus petites que ont est déjà dans un régime non-linéaire de croissance des structures puisque . Intuitivement, on comprend également que puisque les structures s’effondrent gravitationnellement au cours du temps, la variance du champ de matière augmente donc la normalisation de également (Figure 7).
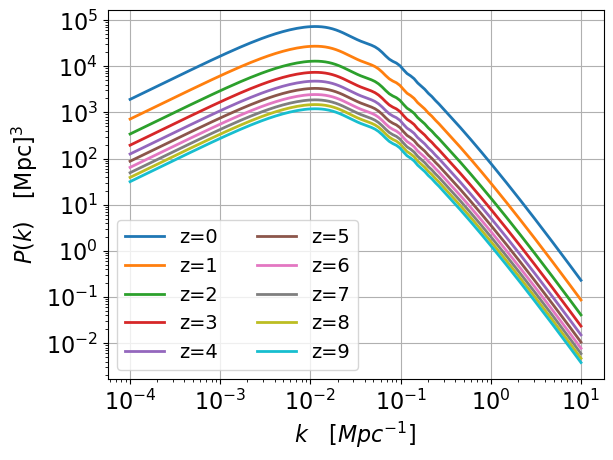
Figure 7:Évolution du spectre de puissance de la matière linéaire avec le redshift.
Ondes acoustiques dans l’Univers primordial¶
Avant le découplage, des ondes acoustiques parcourent le plasma primordial. Définissons l’horizon sonore comobile comme :
la distance comobile maximum parcourue par une onde acoustique depuis le début de l’Univers. Au moment du découplage, elle vaut soit . C’est donc la distance qu’a pu parcourir une onde issue d’une surdensité présente au Big Bang. Cette propagation des ondes se traduit par une corrélation positive sur la présence de matière à cette échelle spatiale fondamentale. Cette échelle se convertit en séparation angulaire sur le ciel, imprimée sur la carte des anisotropies de température du CMB et donnée par :
Une échelle dans l’espace des distances donne un spectre de puissance de forme sinusoïdale dans l’espace réciproque. La mesure de la position des maxima dans le spectre de puissance des anisotropie de température du CMB permet d’aboutir à une mesure précise de l’horizon sonore Tristram, M. et al., 2024:
La mesure de l’amplitude du spectre ainsi que la pente aux grandes échelles (petits de Figure 10) permet de remonter aux paramètres du spectre de puissance initial :
On note que est proche de 1, confirmant l’intuition initiale du spectre de Harisson-Zel’dovitch. Le fait que est légèrement inférieure à 1 (à plus de 5\sigma) est une signature des modèles d’inflation (voir chapitre suivant). Enfin, le fait que le second pic soit atténué par rapport au premier et troisième pic est une signature de la présence des baryons, ce qui permet de mesurer :
Figure 8:Evolution temporelle de 10 pics Gaussien sous l’effet de la propagation acoustique.
Figure 9:Evolution temporelle d’un champ Gaussien avec un spectre de puissance initial . A gauche, l’évolution de la carte. Au centre, l’empilement de 1000 vignettes centrés sur des pics initiaux. A droite, l’évolution du spectre de puissance.
Figure 10:Spectre de puissance des fluctuations de température du CMB en fonction du mode angulaire Tristram, M. et al., 2024.
:name: fig:desi_peaks :align: center :width: 60%
Illustration de la formation des BAO dans la distribution des galaxies. Credit: DESI collaboration
Conditions initiales adiabatiques ou isocourbures?
Les fluctuations initiales peuvent être soit adiabatiques soit isocourbures. Dans le cas adiabatique, on a égalité des fluctuations pour toutes les composantes de l’Univers : , et on prédit la présence de toutes les harmoniques (1,2,3,...) dans le spectre de puissance du CMB. Dans le cas isocourbure, la fluctiation de densité totale est nulle donc on a des opposition du type . On prédit alors la présence des pics impairs seulement dans le spectre du CMB (1,3,5,...). La présence de tous les pics indique que les conditions initiales étaient adiabatiques (Hu & Sugiyama (1995) p. 27).
Peut-on voir le CMB évoluer dans le temps ?
A retravailler : https://
Sur quelle échelle de temps devrions-nous alors nous attendre à voir le CMB changer ? Les plus petites échelles que nous pouvons résoudre, actuellement, sont d’environ dans le ciel, ce qui correspond à environ \num{50 000} années-lumière (15,\kpc$) à la distance du CMB.
Pour une structure de \num{50 000} années-lumière, la lumière de l’extrémité la plus éloignée met \num{50 000} ans de plus à nous atteindre que la lumière de l’extrémité la plus proche. Cela signifie-t-il que nous devrions nous attendre à ce que les fluctuations de température du CMB à ces échelles changent en environ \num{50 000} ans ? Eh bien, pas tout à fait. Le CMB est décalé vers le rouge d’un facteur de 1100, ce qui signifie que son évolution apparente dans le temps est dilatée par le même facteur. Nous nous attendons donc à ce que les fluctuations aux échelles (actuellement) les plus petites résolues changent sur une échelle de temps (1100 fois plus longue) d’environ 55 millions d’années.
Profondeur optique¶
On définit la profondeur optique par le rapport du nombre de photons reçus sur Terre sans avoir subis aucune diffusion Thomson sur le nombre de photons émis à un instant :
avec
Le temps pour lequel est appelé temps de dernière diffusion. C’est le temps depuis lequel un photon du CMB n’a plus interagi avec un électron. Plus précisément,
C’est un des six paramètres du modèle standard CDM. En effet, après l’émission du fond diffus cosmologique, on entre dans les Ages Sombres de l’Univers, où l’Univers est transparent mais aucun astre n’émet encore de lumière. Mais avec la naissance des premières étoiles et galaxies, peut-être 150 millions d’années après le Big Bang, le milieu neutre est de nouveau ionisé. Bien que très peu dense, les photons du CMB interagissent de nouveau avec les électrons par diffusion Thomson, ce qui diminue l’amplitude des anisotropies de petites échelles dans le spectre de puissance du CMB, et introduit de nouvelles anisotropies dans les anisotropies de polarisation. C’est le paramètre le moins bien mesuré du modèle CDM pour le moment (Figure 12) Tristram, M. et al., 2024, mais il informe sur l’apparition des premiers astres lumineux (Figure 13).
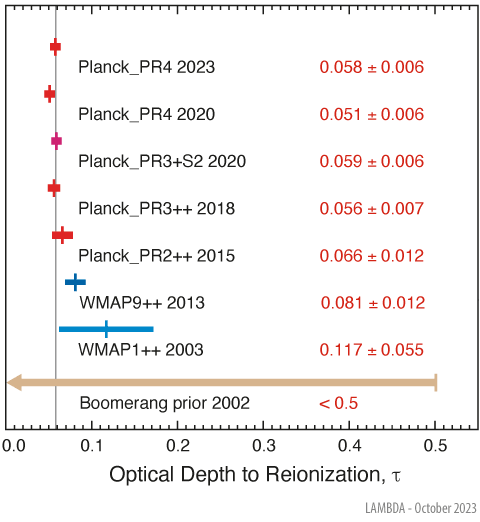
Figure 12:The optical depth to reionization measured as a smearing of the CMB angular power spectrum (d’après https://
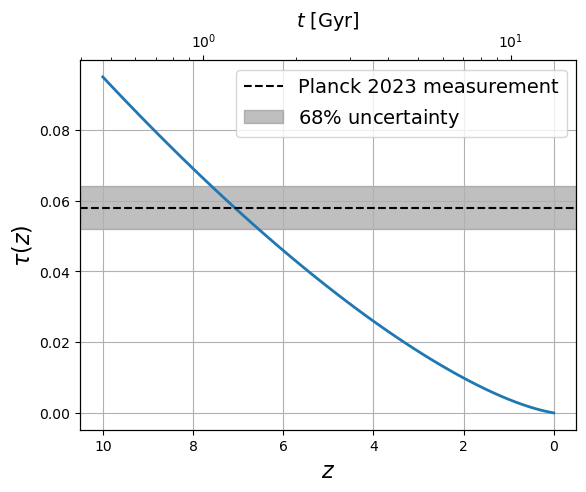
Figure 13:En supposant que l’Univers est de nouveau complètement ionisé, le calcul de sa profondeur optique montre que si aujourd’hui on mesure alors la reionization de l’Univers devait être complète autour de donnant un début de la formation des galaxies antérieure à 1 milliard d’années après le Big Bang.
- Einstein, A. (1917). Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitzungsberichte Der Königlich Preussischen Akademie Der Wissenschaften, 142–152. https://adsabs.harvard.edu/pdf/1917SPAW.......142E
- Weinberg, S. (1989). The cosmological constant problem. Reviews of Modern Physics, 61(1), 1–23. 10.1103/RevModPhys.61.1
- (1902). Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 199(312–320), 1–53. 10.1098/rsta.1902.0012
- Harrison, E. R. (1970). Fluctuations at the Threshold of Classical Cosmology. Physical Review D, 1(10), 2726–2730. 10.1103/physrevd.1.2726
- Zeldovich, Y. B. (1972). A Hypothesis, Unifying the Structure and the Entropy of the Universe. Monthly Notices of the Royal Astronomical Society, 160(1), 1P-3P. 10.1093/mnras/160.1.1p
- Chabanier, S., Millea, M., & Palanque-Delabrouille, N. (2019). Matter power spectrum: from Ly α forest to CMB scales. Monthly Notices of the Royal Astronomical Society, 489(2), 2247–2253. 10.1093/mnras/stz2310
- Tristram, M., Banday, A. J., Douspis, M., Garrido, X., Górski, K. M., Henrot-Versillé, S., Hergt, L. T., Ilić, S., Keskitalo, R., Lagache, G., Lawrence, C. R., Partridge, B., & Scott, D. (2024). Cosmological parameters derived from the final Planck data release (PR4). A&A, 682, A37. 10.1051/0004-6361/202348015
- Hu, W., & Sugiyama, N. (1995). Toward understanding CMB anisotropies and their implications. Physical Review D, 51(6), 2599–2630. 10.1103/physrevd.51.2599