On distingue deux types de mesures cosmologiques: les mesures de distance qui cartographient l’histoire de l’expansion de l’Univers, et les mesures de croissance des structures qui décrivent l’évolution des grandes structures de l’Univers. Les premières sont des données simples qui in fine reviennent à mesurer l’évolution du paramètre de Hubble . Deux méthodes sont utilisées. La première méthode historiquement mise en œuvre utilise des chandelles standard, via des supernovæ de type Ia. Si on sait d’une catégorie d’objets astrophysiques qu’ils ont tous la même luminosité intrinsèque, alors si cet objet apparaît faible, c’est qu’il est situé loin et on peut en déduire sa distance à partir de sa luminosité apparente. La seconde méthode utilise une règle standard, à comprendre une longueur caractéristique invariante que l’on peut mesurer tout le long de l’histoire de l’Univers. Si cette longueur apparaît plus petite qu’aujourd’hui à un certain redshift , alors sachant qu’elle n’a pas dû évoluer (ou sachant comment elle a évolué), on peut en connaître sa distance. Cette méthode est utilisée dans les oscillations baryoniques acoustiques et la mesure du spectre de puissance angulaire du fond diffus cosmologique. Le principe de ces deux méthodes est illustré Figure 1.

Figure 1:Principe de la mesure de l’expansion de l’Univers par l’utilisation de chandelles standard (les supernovæ de type Ia) et d’une règle standard (distance moyenne entre galaxies, issue de la distance moyenne entre sur-densités du fond diffus cosmologique).
1Principe de la méthode des chandelles standard¶
La méthode des chandelles standard s’appuie sur la mesure des flux lumineux venant d’astres de luminosités intrinsèques identiques. Pour mesurer la vitesse d’expansion de l’Univers, il faut disposer de distances de luminosité associées à des redshifts et ainsi construire un diagramme de Hubble-Lemaître.
La Apparent magnitude est une échelle logarithmique qui mesure la luminosité d’un objet observé depuis la Terre. Elle repose sur la mesure d’un flux lumineux acquis avec un télescope équipé d’un capteur photosensible (/s/m) ou un bolomètre (W/m), comparé à un flux de référence qui fixe l’échelle. Historiquement, ce flux de référence s’appuie sur une étoile étalon, Véga dans la constellation de la Lyre. Pour se raccorder aux 6 catégories de magnitudes définies dans l’Antiquité, la magnitude apparente d’un astre est définie par :
La magnitude absolue est le flux qu’on recevrait de cette source de luminosité observée à une distance de :
Dans un monde idéal, il suffirait de mesurer les flux d’une collection de chandelles standard à des redshifts et de les comparer entre eux pour obtenir une relation entre distance de luminosité et redshift. En effet, la magnitude apparent d’une chandelle standard de redshift est liée au taux d’expansion via la distance de luminosité:
On appelle module de distance la quantité :
C’est la baisse de luminosité en magnitude liée à la distance de l’astre. Si une chandelle standard est 2 fois plus loin alors elle apparait 4 fois moins brillante et son module de distance augmente de 1.5 magnitude. Par la mesure des flux, on peut ainsi estimer les distances relatives entre les chandelles standard.
Le point le plus important à remarquer dans cette formule est que la vitesse d’expansion cosmologique est inscrit dans la forme de la courbe , et non dans sa normalisation. La normalisation de la courbe dépend notamment de et . La méthode des chandelles standard permet donc de mesurer l’évolution de l’expansion de l’Univers, sans avoir besoin de connaître leur luminosité absolue ! En revanche, si on connaît leur luminosité absolue , alors on peut établir une échelle de distances absolues et la normalisation du diagramme de Hubble donne accès à la valeur de (Figure 2).

Figure 2:Module de distance en fonction du redshift pour trois modèles cosmologiques. Un changement des paramètres modifie la forme de la courbe alors que le paramètre modifie sa normalisation.
2Diagramme de Hubble des supernovae¶
Pour établir un diagramme de Hubble sur des distances cosmologiques, il faut disposer de sources de luminosités identiques et visibles sur de très grandes distances. Les galaxies sont de tailles donc de luminosité intrinsèque trop variables pour jouer ce rôle. Cependant, les supernovae de type Ia sont des explosions stellaires dont la luminosité est commensurable à celle d’une galaxie. Elles peuvent donc être visibles de loin mais seulement pendant un certain temps.
Les supernovæ de type Ia¶
Les supernovæ sont classées en deux types: gravitationnelles ou thermonucléaires. Les premières sont les plus connues: elles correspondent à l’explosion d’une étoile massive (plus de 8 fois la masse du Soleil) en fin de vie, laissant un cœur stellaire dense et froid: une étoile à neutrons, voire un trou noir dans les cas extrêmes. Les supernovae de type I sont celles ne présentant pas de raies de l’hydrogène dans leur spectre, alors que les supernovae de type II en contiennent. Parmi les supernovae de type I, celles contenant du silicium sont de type Ia, puis les autres Ib ou Ic.
Les étoiles de masse inférieure à terminent leur vie sous forme de géante rouge. A la fin de la combustion de l’hélium, les couches externes sont dispersées dans le milieu interstellaire sous forme de nébuleuse planétaire (sans forcément produire une explosion intense), laissant le coeur stellaire nu. L’effondrement du coeur est stoppé à cause de la pression de dégénérescence des électrons (et non des neutrons comme dans pour les étoiles à neutrons) et de sa faible masse (typiquement ). Sa température de surface reste longtemps très élevée (environ ), d’où son nom de naine blanche. Il est essentiellement composé de carbone et d’oxygène, l’hélium et l’hydrogène ayant été expulsé dans l’espace. Le rayon typique d’un tel objet est de quelques milliers de kilomètres (comme une planète tellurique).
Cette animation montre l’explosion d’une naine blanche, vestige extrêmement dense d’une étoile qui ne peut plus brûler de combustible nucléaire en son cœur. Dans cette supernova de type Ia, la gravité de la naine blanche dérobe de la matière à un compagnon stellaire proche. Lorsque la naine blanche atteint une masse estimée à 1.4 fois la masse actuelle du Soleil, elle ne peut plus supporter son propre poids et explose. Credit: NASA/JPL-Caltech
D’après une étude du Very Large Telescope, environ 75% des étoiles massives vivent dans des systèmes binaires Sana et al., 2012. Dans certains cas, une naine blanche peut donc être liée gravitationnellement à une autre étoile qui, si elle est suffisamment proche, peut voir ses couches externes aspirées par la gravité de la naine blanche. Lorsque la naine blanche a accumulé trop de matière venant de son voisin et approche la masse de Chandrasekhar (), elle devient instable. Les conditions de pression et de température au c\oeur de la naine blanche permettent le réallumage de la fusion du carbone. La naine blanche ne peut se dilater et se refroidir à cause de la pression de dégénérescence des électrons, indépendantes de la température (effet quantique). La réaction s’emballe en une flamme thermonucléaire qui vaporise l’astre en quelques secondes. L’explosion enrichit le milieu interstellaire en éléments de masse intermédiaire (oxygène, calcium, magnésium, silicium, soufre) et de la famille du fer (nickel, cobalt). Ce scénario d’explosion ne reste toutefois qu’une hypothèse dans la mesure où aucune preuve n’existe encore. D’autres scénarios existent comme la fusion de deux naines blanches Nomoto et al., 2013.
Les SNe Ia puisent leur énergie de la désintégration des éléments du groupe du fer qui ont été produits lors de l’explosion Colgate & McKee (1969). Le principal élément radioactif formé est le :
puisqu’il est une combinaison stoechiométrique simple d’atomes de carbone et d’oxygène, les atomes les plus abondants d’une naine blanche. L’isotope du nickel se désintègre ensuite en avec une demi-vie de 6.1 jours, qui lui même se désintègre en fer stable avec une demie-vie de 77.3 jours :
La luminosité totale est estimée à soit environ celle d’une galaxie (voir photographies Figure 4 et Figure 5). Ce sont donc des objets a priori visibles à des distances cosmologiques. Comme l’explosion se produit systématiquement à la même masse stellaire, à peu près la même quantité de matériaux est rejetée dans l’espace et émet la même quantité de lumière. De plus, la composition des naines blanches étant très standard, la composition de la matière émettrice est la même. Elles ont donc toutes à peu près la même luminosité totale intrinsèque. Cependant ce sont aussi des événements transitoires: la durée d’une supernova est de quelques dizaines de jours. Pour la capter, il faut donc regarder le ciel au bon endroit et au bon moment.
Les supernovæ de type Ia (SNe Ia) sont les premières sondes cosmologiques qui ont permis de mesurer l’expansion de l’Univers sur des distances cosmologiques, et découvrir son expansion accélérée Riess et al., 1998Perlmutter et al., 1999. Le prix Nobel de physique a été décerné en 2011 à Saul Perlmutter, Brian Schmidt et Adam Riess pour cette découverte majeure.

Figure 4:La supernova SN 1994D (le point blanc brillant en bas à gauche de l’image), dans la galaxie spirale NGC4526.

Figure 5:La supernova sn2023ixf découverte par le relevé ZTF et photographiée par le télescope StarDICE (Newton, diamètre cm) dans 4 filtres le 25 mai 2023.
Séquences spectrales et courbes de lumière¶
Une supernova de type Ia reste visible environ 40 jours dans le ciel dans le visible. Pour reconnaître son type, il faut l’observer sous plusieurs couleurs et si possible acquérir son spectre. Une séquence de spectres acquises sur une supernovæ de type Ia est présentée Figure 7.
Série d’images de l’explosion d’une supernova de type Ia. La supernova, SN 2015F, s’est produite dans la galaxie NGC 2442 au début du mois de mars 2015, à une distance d’environ 80 millions d’années-lumière de la Terre. Des images quotidiennes de février 2015 à octobre 2015 ont été combinées pour créer ce film. Les images ont été prises avec un télescope robotique de 17 pouces en Australie.
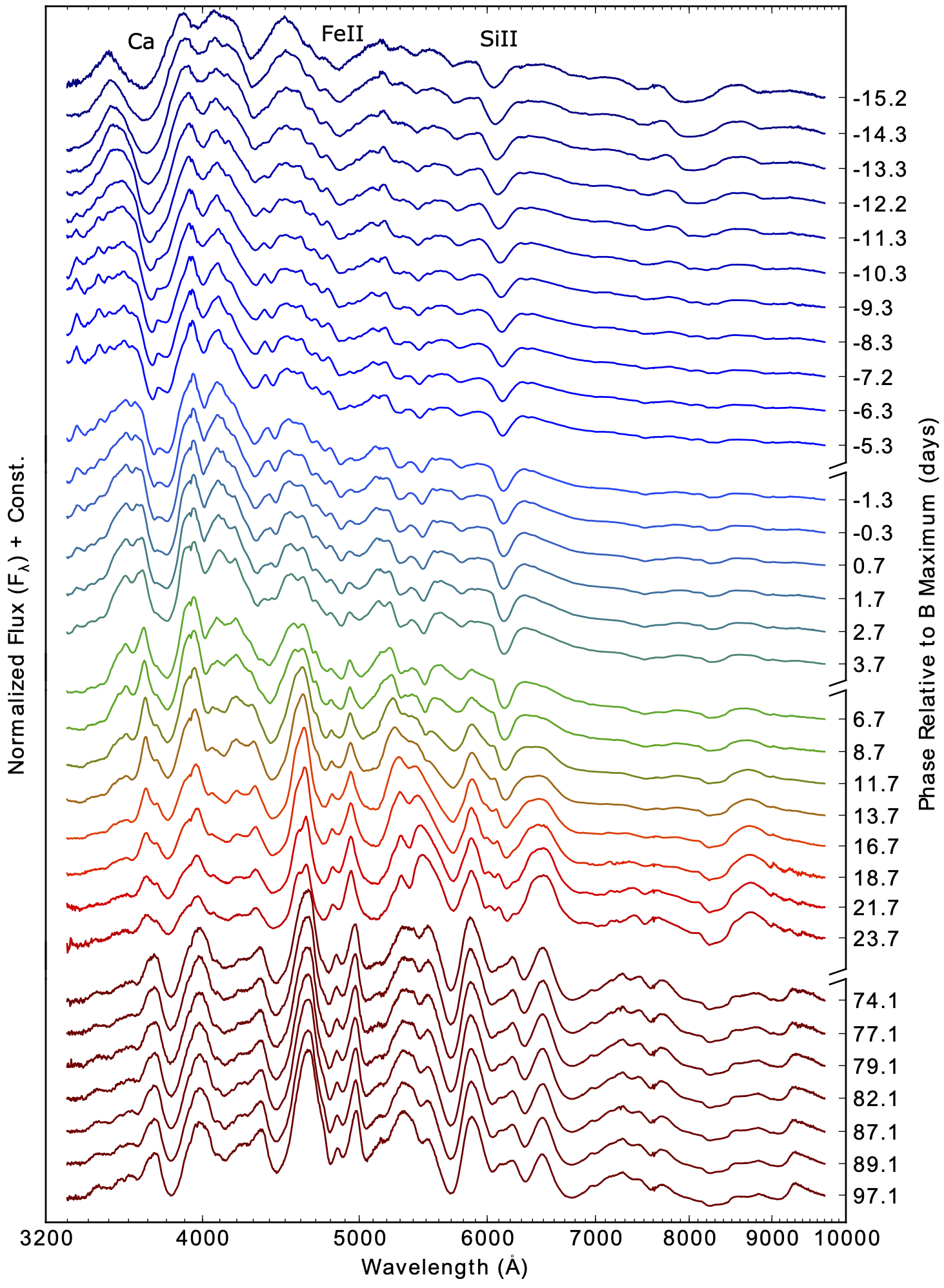
Figure 7:Série spectro-temporelle de SN2011fe mesurée par le relevé SNfactory Pereira et al., 2013. Les noms des principales composantes du spectre sont indiqués dans la partie supérieure de la figure.
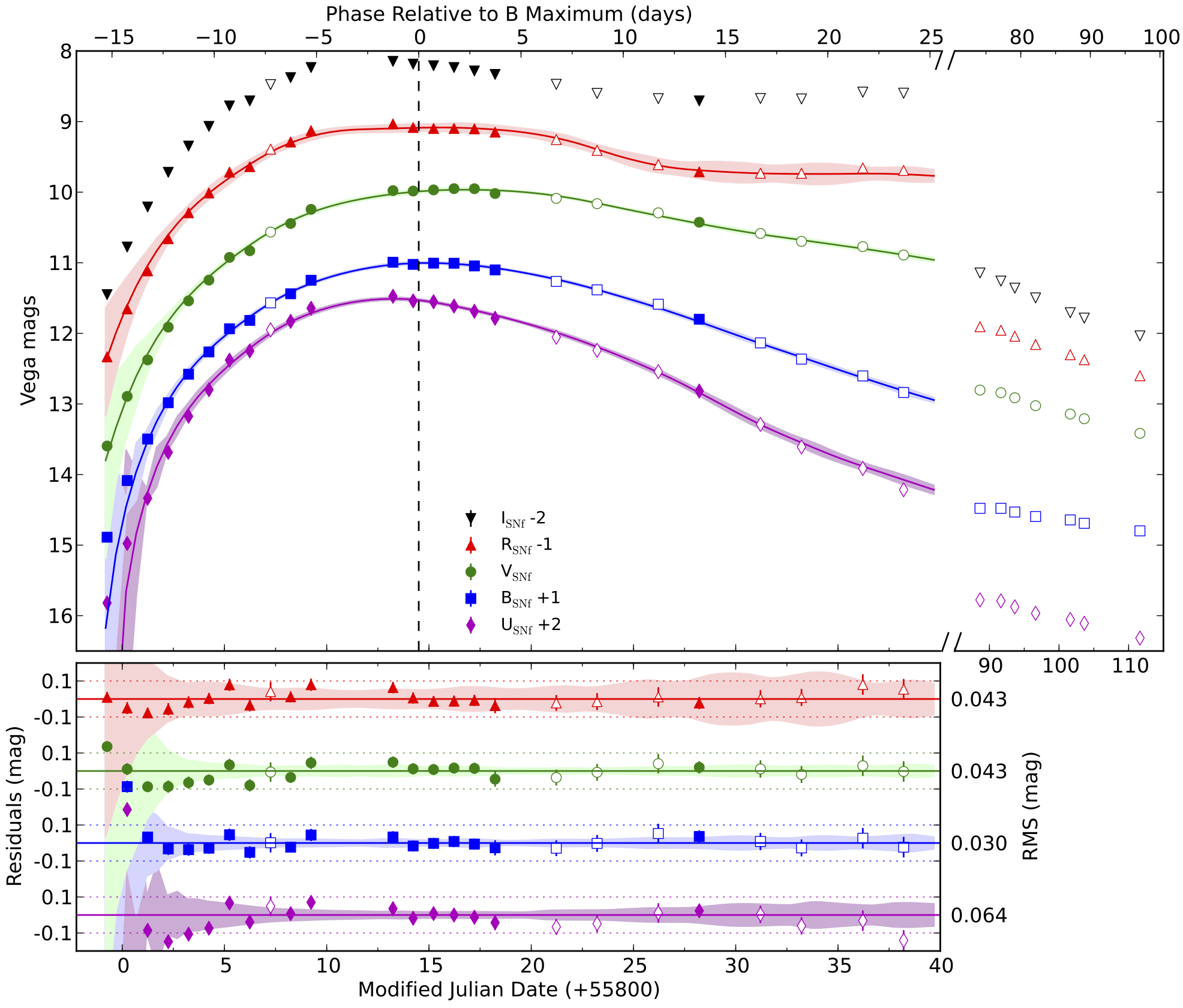
Figure 8:Courbes de lumière synthétisées SN2011fe en utilisant le jeu de filtres UBVRI Pereira et al., 2013. Les symboles remplis et ouverts correspondent respectivement aux nuits photométriques et non photométriques. Les résultats d’un ajustement simultané SALT2 de UBVR dans la plage de dans l’intervalle de phase jours sont représentés par des lignes pleines, avec les résidus correspondants (SALT2 - SNf) sur le panneau inférieur. Les zones ombrées représentent l’erreur du modèle SALT2. La rupture dans l’axe du temps correspond à l’écart de jours dans le suivi pendant lequel SN2011fe n’était pas visible pendant la nuit depuis Hawaii. Notez le changement d’échelle de l’axe temporel étendu couvrant les observations tardives.
En pratique, nous ne possédons pas de séquences spectrales aussi précises que celle présentée Figure 7 pour chaque supernova détectée, car cela coûte trop de temps d’observation sur les plus grands télescopes au monde équipés de spectrographe. Seul le relevé SNFactory a dédié un spectrographe à l’étude spectrale systématique des supernovae. En règle générale, si possible, un seul spectre de la supernova est acquis autour de son maximum de luminosité (car c’est plus aisé) afin de vérifier que c’est bien une type Ia (spectre d’identification), avec un spectrographe qui n’a pas besoin d’avoir une grande résolution pour identifier les raies principales de l’explosion thermonucléaire. Plus tard, un spectre de la galaxie hôte est pris pour mesurer son redshift précisément s’il n’est pas déjà connu, avec un spectrographe à plus haute résolution (spectre de redshift).
La principale information disponible sur une supernova de type Ia est donc sa courbe de lumière, c’est-à-dire la séquence temporelle des flux lumineux, mesurée par un télescope avec différents filtres passe-bande équipant la caméra du télescope Figure 8.
Il faut donc définir un instant où comparer la brillance des chandelles standard et un filtre de référence. Pour des raisons pratiques, on utilise comme référence les magnitudes au maximum de l’émission. Pour des raisons historiques, on utilise la bande Johnson B comme filtre de référence. La magnitude du maximum de luminosité d’une supernova de type Ia observée en bande B est donc utilisée comme chandelle standard, ou du moins standardisable.
Systèmes photométriques
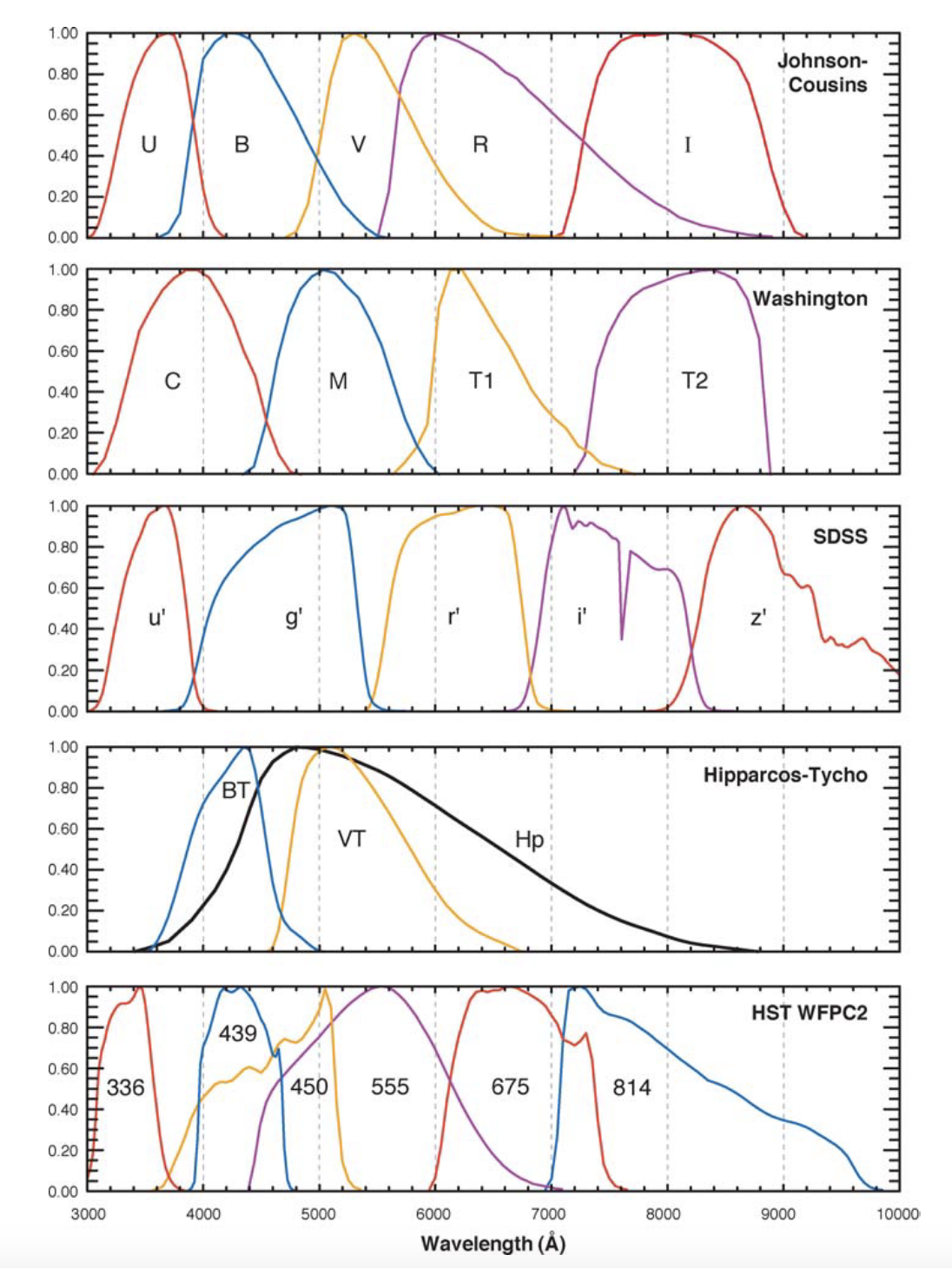
Figure 9:Filtres passe-bande pour différents systèmes photométriques Bessell, 2005.
Les relevés astrophysiques et cosmologiques en photométrie sont intéressés par mesurer la couleur des objets pour accéder à leurs propriétés physiques. Pour cela, les télescopes sont équipés de filtres passe-bande, dont les formes et positions dépendent des technologies utilisées et des besoins du relevé.
Un système photométrique standard est défini par une liste de magnitudes et de couleurs standard mesurées à des bandes passantes spécifiques pour un ensemble d’étoiles bien réparties dans le ciel. Les magnitudes observées sont corrigées pour tenir compte de l’atténuation de l’atmosphère terrestre loin du zénith, et les données sont ensuite normalement extrapolées à une masse d’air nulle (en dehors de l’atmosphère).
Le système UBV est l’un des systèmes photométriques photoélectriques standard les plus anciens et les plus utilisés Johnson & Morgan (1953). La bande B a été conçue pour se rapprocher de la magnitude photographique brute (moins les UV), tandis que la bande V a été conçue pour se rapprocher du système de magnitude visuelle. Les systèmes photométriques des relevés modernes SDSS et LSST utilisent plutôt des filtres interférentiels nommés ugrizy dans le visible et proche infrarouge.
Magnitude dans le référentiel au repos¶
Les flux lumineux exprimés en (/s/m) ou (W/m) sont dits bolométriques[1] car intégrés sur tout le spectre. Malheureusement la capacité à mesurer cette quantité dépend du capteur utilisé. Dans le visible et l’infrarouge, les capteurs sont basés sur l’effet photoélectrique donc ils sont transparents au-dessus d’une certaine longueur d’onde. Dans le visible et l’infrarouge, les flux mesurés ne peuvent être bolométriques.
De plus, beaucoup d’information peut être tirée de la mesure de la couleur d’un objet, comme le type de la supernova : pour cela il faut l’observer à travers différents filtres passe-bande et comparer les flux.
On introduit la densité spectrale d’énergie d’un astre exprimée[2] en W/m/nm. Notons la transmission de l’instrument équipé d’un filtre . Le flux mesuré est alors :
où est la longueur d’onde des photons incidents. Alors la définition de la magnitude apparente pour un filtre devient :
avec la densité spectrale de flux de la source de référence (Véga par exemple). La magnitude absolue en filtre est la magnitude de l’astre en filtre si on l’observait dans son référentiel au repos à :
avec la luminosité spectrale (en W/nm).
On note la transmission du filtre B dans le système photométrique de Johnson UBV (voir encadré). Alors on pose:
La magnitude absolue dans la bande est :
Cependant, les télescopes ne sont pas tous équipés d’un filtre B. De plus, et c’est la raison principale, le maximum d’émission se déplace en longueur d’onde avec le décalage vers le rouge donc il faudrait pouvoir décaler vers le rouge le filtre B pour capter la même portion de spectre (Figure 10). Comme nous voulons comparer l’effet de la distance uniquement pour cartographier , ces effets de décalage en longueur d’onde doivent pourtant être supprimés pour standardiser et comparer le flux observé au maximum d’émission. Historiquement, pour les supernovæ de type Ia, les cosmologistes établissent les magnitudes apparentes en bande B dans le référentiel au repos de la supernova. La magnitude est donc la magnitude apparente dans le référentiel au repos en bande B, comme s’il n’y avait pas d’expansion mais seulement un effet de distance.
La chandelle standard est le maximum d’émission des supernovæ de type Ia dans la bande comme si elle était observée dans son référentiel au repos.
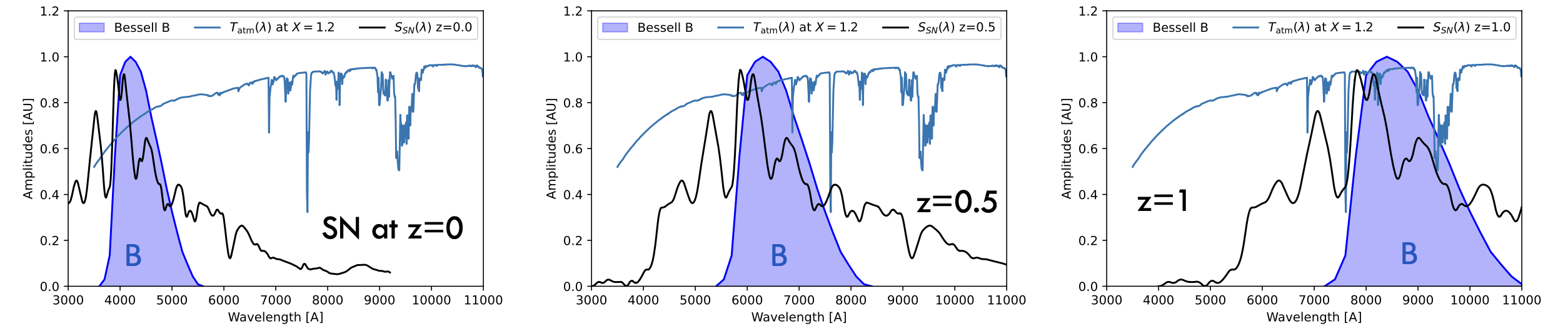
Figure 10:Magnitudes apparentes en bande pour des supernovæ à différents redshifts: elles correspondent à l’intégrale de la densité spectrale de la supernova à son maximum dans la bande redshiftée.
Comme ce n’est pas possible de réaliser une observation dans le référentiel au repos de la supernova, cette magnitude doit être calculée à partir des observations dans des filtres quelconques et d’un modèle spectrophotométrique de la supernova.
Modèle spectrophotométrique¶
Le modèle spectrophotométrique va être la donnée de la densité spectrale en fonction du temps , déterminée sur les données (la collection des courbes de lumière et des spectres disponibles). Supposons qu’on est capable de l’obtenir, après un entrainement sur les données, comme avec le modèle SALT2 Guy et al., 2007. Comment pouvons-nous transformer les magnitudes apparentes observées en magnitudes en bande B dans le référentiel au repos ?
Tout d’abord, il faut étudier l’effet du redshift sur les densités spectrales. Le flux et la luminosité intrinsèque (en W) d’un astre situé au redshift sont reliés par :
avec la distance de luminosité. Tous les photons reçus dans une étroite gamme de fréquences logarithmiques centrée sur la longueur d’onde observée ont été émis dans une gamme de longueur d’onde centrée également étroite centrée sur . L’équation (12) relie donc ainsi les densités spectrales de flux aux luminosités spectrales en présence d’un redshift Condon & Matthews, 2018:
Cette relation donne le lien entre la densité spectrale de flux observée à et la densité spectrale de luminosité émise à .
Maintenant, recherchons comment transformer les magnitudes observées en magnitudes , à partir de la définition de la magnitude apparente en bande :
Posons la -correction en bandes et Hogg et al., 2002 :
Alors la magnitude apparente peut se décomposer en trois termes :
et la magnitude se calcule à partir des observations et de la -correction calculée :
La -correction représente bien la correction en magnitude qu’il faut apporter si on observait l’astre dans son référentiel au repos et avec un autre filtre. Après l’application de la -correction, le diagramme de Hubble se modélise simplement par :
une équation très similaire à (3). Le membre de gauche représente les magnitudes acquises par le télescope et transformées en bande au repos et au maximum. Le membre de droite représente le modèle cosmologique explicatif. Pour les SNe Ia, Betoule et al., 2014. On voit donc que la dépendance en distance est entièrement contenue dans le module de distance , mais remarquons qu’il existe une dépendance en redshift supplémentaire dans la -correction. Il faut donc savoir correctement modéliser pour ne pas introduire de biais en redshift dans le diagramme de Hubble.
Malheureusement, la -correction dépend d’un certain nombre d’ingrédients qu’il faut donc connaître au préalable pour la calculer :
le redshift , à inférer depuis un spectre;
la densité spectrale de la supernova, à construire par un modèle spectrophotométrique ajusté sur les séquences spectrales mesurées (comme dans la Figure 7) comme SALT2 Guy et al., 2007;
la densité spectrale de référence , à établir par mesure (Hayes et al. (1975), Souverin et al. (2024)) ou modélisation d’atmosphère stellaire Bohlin et al. (2014);
la transmission des filtres du télescope , voire de la transmission atmosphérique du lieu .
Pour obtenir une mesure du paramètre d’état de l’énergie noire au pourcent, il faut donc que chacun de ces ingrédients soit établi à mieux que le pourcent. Aujourd’hui, les incertitudes dominantes sur la mesure de par les supernovae de type Ia sont les incertitudes systématiques de calibration photométrique, donc la connaissance de la bande passante des filtres des instruments ainsi que la connaissance des flux de références Betoule et al., 2013Scolnic et al., 2018 .
Standardisation¶
Après -correction, on peut comparer les magnitudes à un modèle cosmologique. Avec les données JLA du SuperNova Legacy Survey, on obtient le diagramme de Hubble Figure 11.
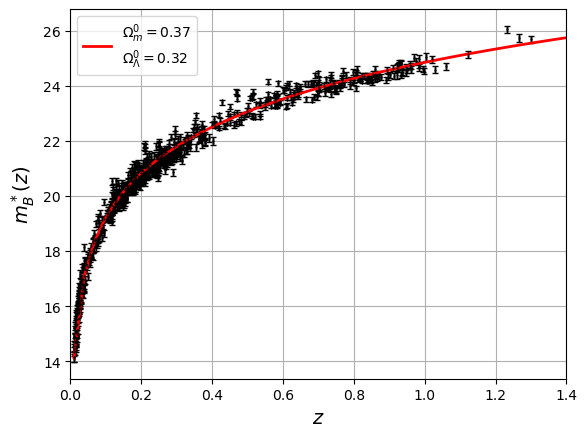
Figure 11:Diagramme de Hubble des 740 SNeIa du relevé SNLS, comparé à un modèle CDM avec et .
Autour du diagramme, on observe que les résidus au diagramme de Hubble ont une dispersion de mag, supérieures aux erreurs de mesure. Si on trace ces résidus en fonction de la couleur ou de la durée normalisée de la supernova, on s’aperçoit qu’ils sont corrélés (Table 1).
Table 1:Résidus au diagramme de Hubble colorés en fonction de la durée normalisée (gauche) ou de la couleur (droite).
Source:Type Ia supernovae 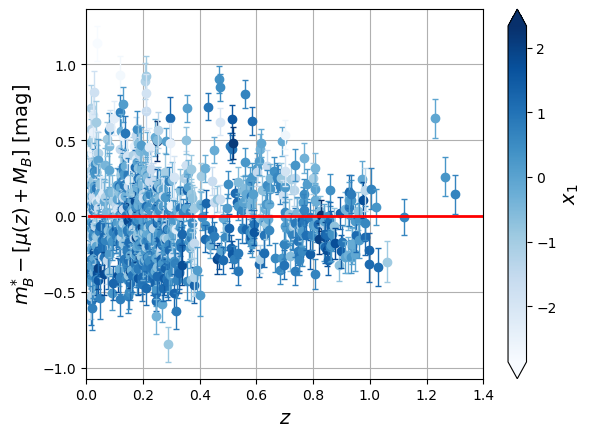 | Source:Type Ia supernovae 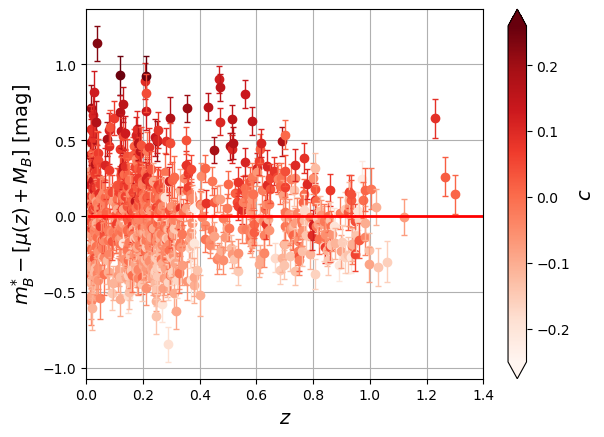 |
Il y a donc une variabilité des supernovae qui n’a pas été prise en compte dans notre modèle spectrophotométrique jusqu’à présent.
On observe que plus la courbe de lumière dure dans le temps, plus elle est brillante à son maximum (règle du brighter-slower). De plus, plus les SNIa sont bleues, plus elles sont brillantes également (règle du brighter-bluer). Il y a aussi un effet d’environnement qui lie la brillance de la supernova et la masse de la galaxie hôte.
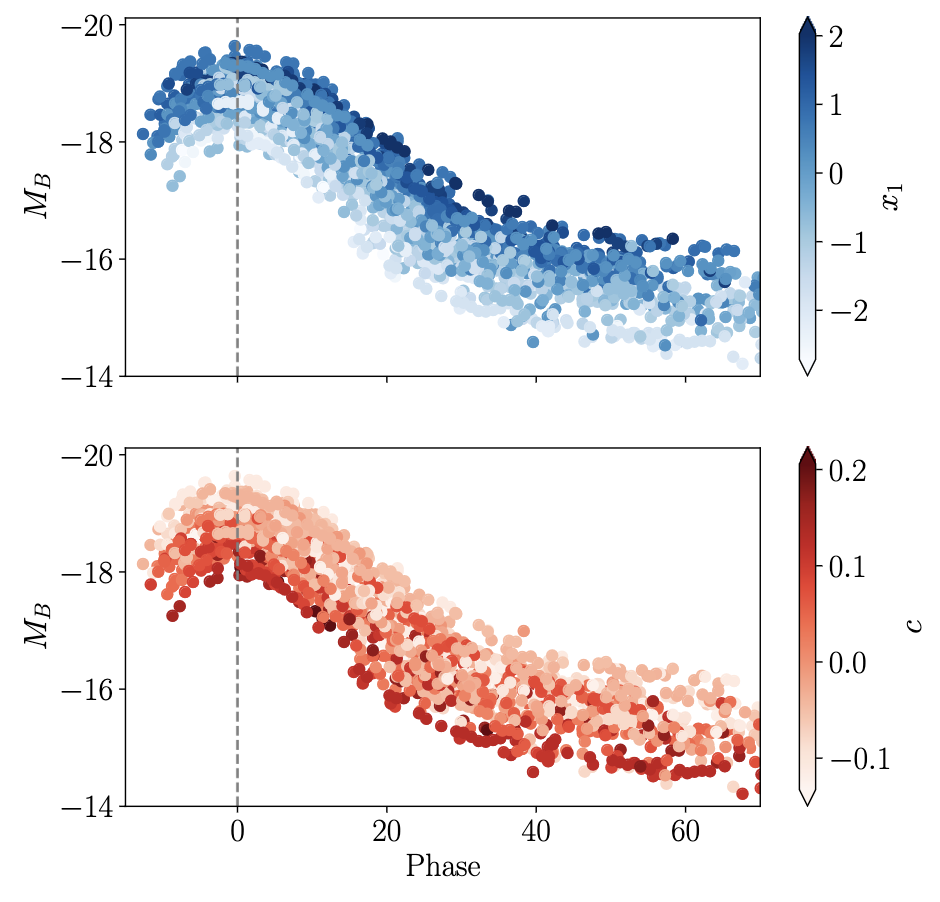
Figure 12:Courbes de lumière de SNe Ia du lot de données JLA du relevé SNLS colorées en fonction de ou Nicolas, 2022.
Le flux de lumière est lié à la production et à la décroissance de nickel Ni. Les deux relations présentées ci-dessus peuvent ainsi être expliquées qualitativement: plus la SNIa produit de Ni, plus elle sera brillante et plus elle contiendra d’ions FeII et CoII émettant dans le bleu, mais aussi plus elle sera opaque (donc l’émission des photons par diffusion sera retardée, donc la SNIa brillera plus longtemps) Kasen & Woosley, 2007.
Les SNe Ia ne sont donc pas si standard, car leurs courbes de lumière dépendent de la quantité de Ni disponible à l’origine. Néanmoins sans corriger cette dispersion intrinsèque les équipes du Supernova Cosmology Project (SCP) mené par Saul Perlmutter et du High-z Supernova Search Team mené par Brian Schmidt ont pu démontrer l’existence d’une expansion accélérée Riess et al., 1998Perlmutter et al., 1999. Cette dispersion est gênante pour améliorer les mesures d’expansion de l’Univers au niveau du pourcent. Néanmoins, elle se décrit empiriquement par deux relations linéaires pour et avec des coefficients et respectivement. Pour la masse de l’hôte, on ajuste un paramètre augmentant la magnitude pour les supernovae se situant dans des galaxies de masse supérieure à .
Ces trois relations empiriques ajoutent trois paramètres supplémentaires , et à ajuster également sur les données Tripp & Branch (1999):
Après cette standardisation, la dispersion au diagramme de Hubble est réduite à mag ce qui augmente la précision sur les paramètres cosmologiques.
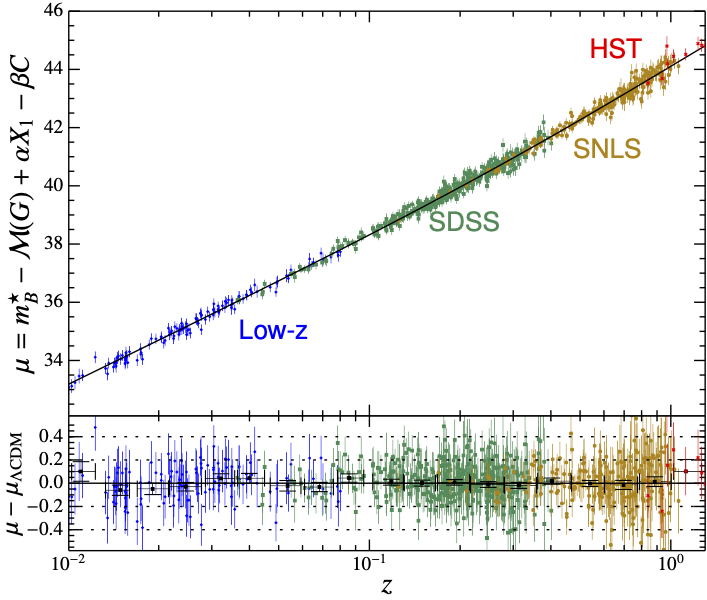
Figure 13:Diagramme de Hubble des supernovæ du catalogue JLA. La courbe noire représente un modèle CDM ajusté aux données. Un modèle sans énergie noire apparaîtrait significativement en dessous de la courbe décrite par les données (mag à ).
Étalonnages¶
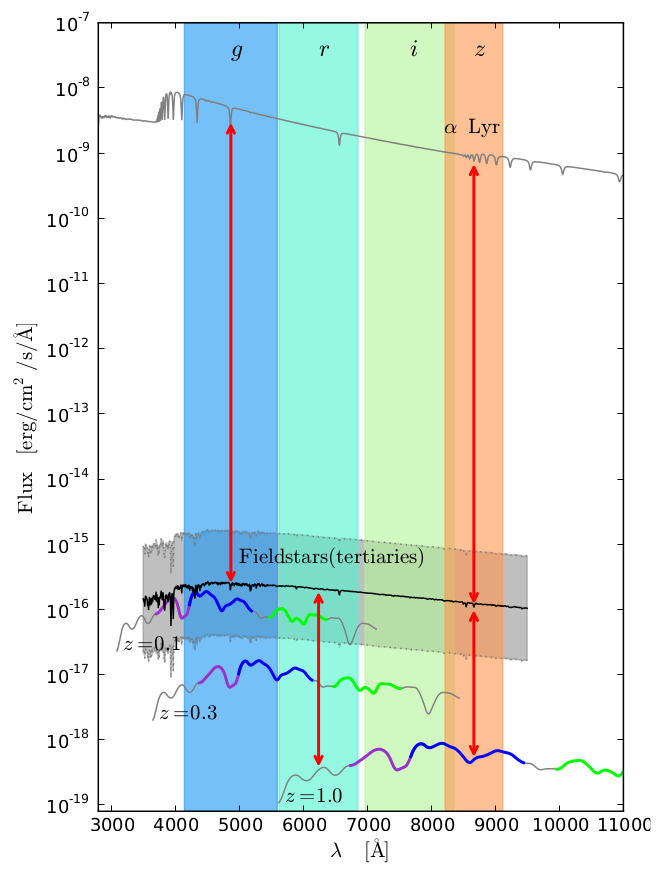
Figure 14:Stratégies pour étalonner la mesure du flux lumineux des étoiles tertiaires (les étoiles secondaires ne sont pas représentées). La bande redshiftée est représentée par un trait bleu épais sur les spectres des SNe Ia.
State of the art¶
3Mesure locale de ¶
Le module de distance permet de mesurer la distance relative entre les SNe Ia, ce qui fournit des informations cruciales sur l’énergie noire. Cependant, la distance absolue des SNe Ia ne peut pas être obtenue par cette méthode : il y a une dégénérescence entre la luminosité de la SNe Ia et lors de l’estimation. Pour briser cette dégénérescence, l’échelle des distances cosmiques est utilisée. Cette méthode implique une série de mesures de distances qui se chevauchent en utilisant divers objets et techniques astronomiques, comme l’illustre la figure 12 de Riess et al. (2022). En ancrant les distances des SNe Ia à des distances mesurées indépendamment par l’échelle des distances cosmiques, nous pouvons démêler la magnitude absolue des SNe Ia de celle de H0. Dans ce qui suit, nous allons discuter des différentes étapes de cette échelle de distance.
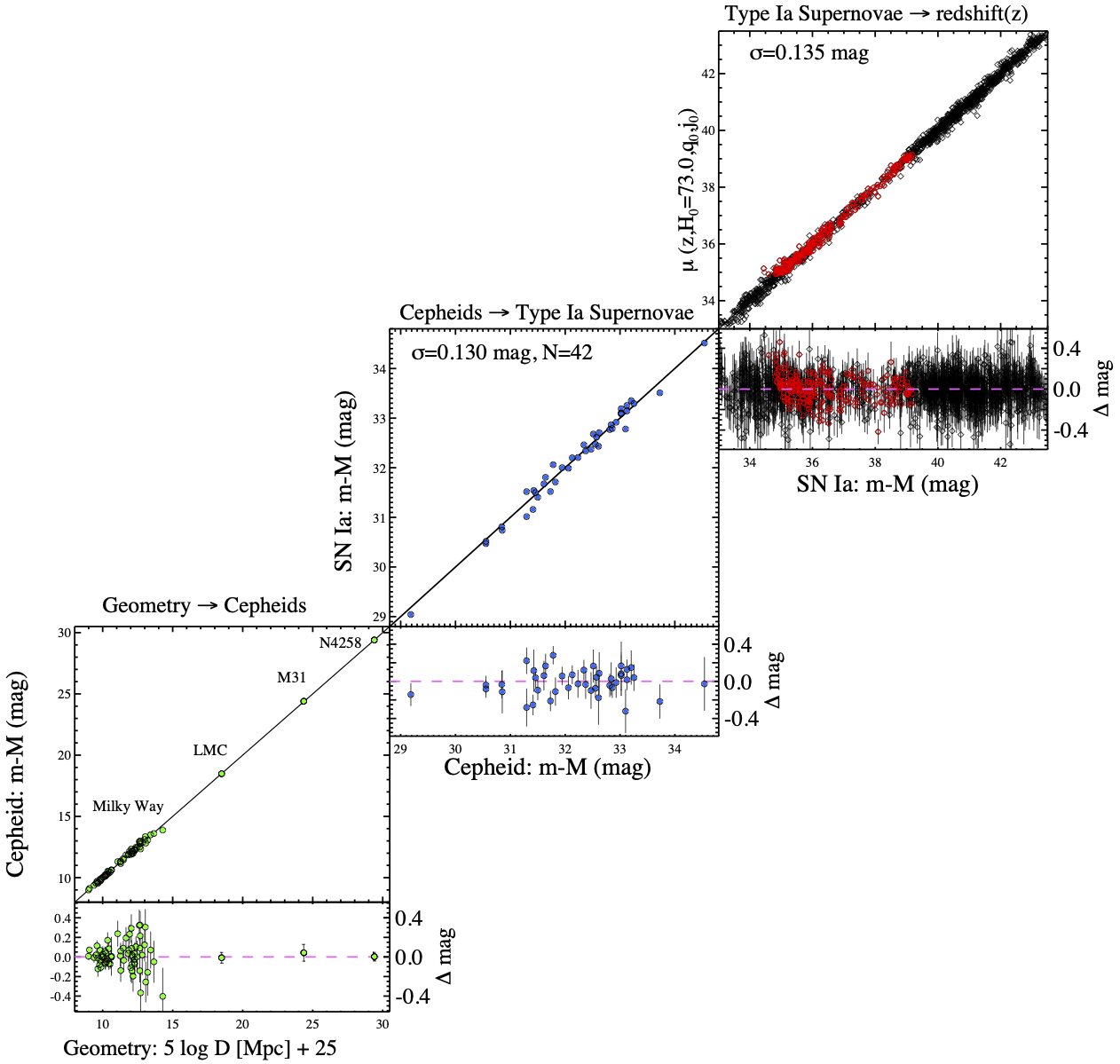
Figure 15:Echelle des distances astrophysiques Riess et al., 2022. Les mesures des paramètres d’orbite dans le Système Solaire permettent de calibrer la mesure des distances des étoiles par la méthode de la parallaxe. La distance de certaines étoiles Céphéides est mesurée par parallaxe ce qui permet d’établir une relation entre le flux des céphéides, leur période de luminosité et leur distance (carré inférieur). La distance obtenue par la luminosité de Céphéides dans des galaxies proches permet de calibrer la luminosité intrinsèque de SNe Ia explosant dans une galaxie contenant des Céphéides (carré intermédiaire). Une fois la luminosité intrinsèque des SNe Ia connue, la mesure de la pente de la relation distance-redshift pour des supernovae lointaines (mais pas trop) permet d’accéder à .
Mesure de la parallaxe¶
Lorsqu’une étoile de premier plan est observée à partir de deux positions opposées, A et B, sur l’orbite de la Terre autour du Soleil, elle semble se déplacer par rapport au champ d’étoiles d’arrière-plan vers des positions A’ et B’. Ce décalage apparent est appelé parallaxe. La distance entre la Terre et le Soleil est définie comme une unité astronomique (UA), c’est-à-dire la moyenne entre les deux demi-axes de l’orbite elliptique de la Terre. Avec cette distance, et en mesurant le déplacement apparent de la position de l’étoile, on peut calculer par trigonométrie la distance entre l’observateur et l’étoile. Ce phénomène est connu sous le nom de parallaxe. Les mesures de parallaxe effectuées par Gaia atteignent une précision de 0.04 mas Luri et al. (2018). Cette méthode constitue le premier barreau de l’échelle des distances cosmiques.
Céphéides¶
Les Céphéides sont un type d’étoile qui pulse radialement, subissant des variations régulières de diamètre et de température. Ces pulsations se traduisent par des changements de luminosité avec une période et une amplitude bien définies et stables. Elles ont été découvertes par Henrietta Swan Leavitt Leavitt, 1907, qui a mis en évidence la corrélation entre le diamètre et la température de l’étoile.
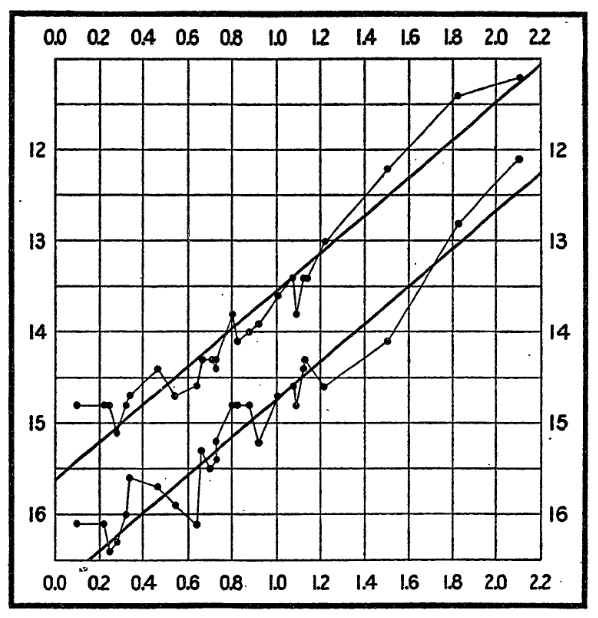
Figure 16:Relation entre la magnitude des minima (courbe basse) et des maxima (courbe haute) des courbes de lumière des Céphéides en fonction du logarithme de leur période de pulsation, d’après Leavitt & Pickering (1912).
La magnitude des maxima ou minima de la courbe de lumière d’une Céphéide est proportionnelle au logarithme de sa période de pulsation. Cette loi est connue sous le nom de loi de Leavitt, et la figure 2 de Leavitt & Pickering (1912), illustre cette relation (Figure 16).
En observant des Céphéides suffisamment proches pour utiliser la méthode de parallaxe pour l’estimation de la distance, nous pouvons calibrer la magnitude absolue des Céphéides, et donc leur relation période-luminosité intrinsèque. En raison de la stabilité de leur fonction période-luminosité, cette calibration peut ensuite être appliquée à toutes les Céphéides, ce qui nous permet de mesurer leur distance de luminosité dans d’autres galaxies où la méthode de la parallaxe n’est pas réalisable. Par conséquent, les Céphéides servent de première chandelle standard dans l’échelle des distances cosmiques, permettant de déterminer la distance d’autres galaxies, comme le montre le graphique central de la Figure 15.
Supernovae de type Ia¶
Une fois que la fonction période-luminosité des Céphéides est calibrée, cette calibration est transférée aux SNe Ia. Pour estimer la distance d’une galaxie à l’aide d’une Céphéide, celle-ci doit être résolue par rapport aux autres sources lumineuses de la galaxie et sa photométrie doit être réalisée (Figure 17). En mesurant sa période de pulsation, on en déduit sa luminosité intrinsèque donc la distance de la galaxie hôte.
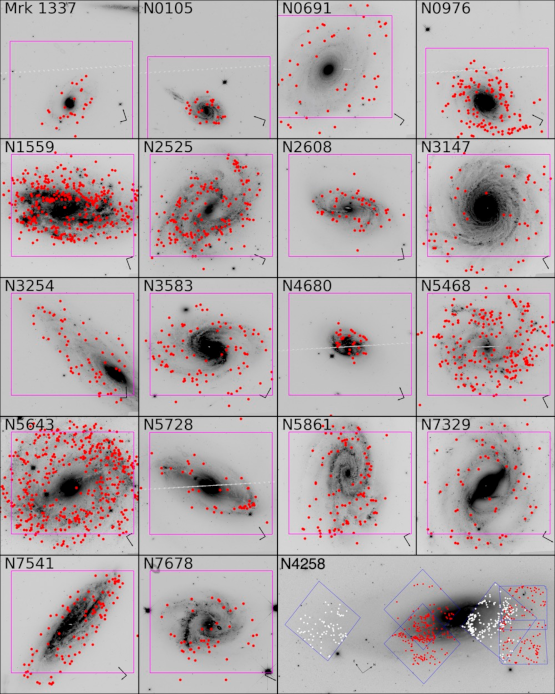
Figure 17:Identification de Céphéides (points rouges) dans 18 galaxies où ont été observées des SNe Ia ainsi que dans le maser NGC4258, par le relevé SHOES du Hubble Space Telescope (d’après Riess et al. (2022)).
Ensuite, l’observation d’une SN Ia dans la même galaxie permet de connaître sa luminosité intrinsèque puisque la distance est connue via la Céphéide. Riess et al. (2022) rapporte l’observation de 42 SNe Ia dans 37 hôtes calibrés. Ces SNe Ia sont représentées dans le carré central de Figure 15, ce qui permet de calibrer la magnitude absolue des SNe Ia. Enfin, le carré supérieur trace un diagramme de Hubble des SNe Ia, qui est directement lié à l’estimation de la distance géométrique par la méthode de la parallaxe.
Avec cet échantillon, Riess et al. (2022) rapporte une mesure de de km/s/Mpc, en tension à plus de avec l’extrapolation des mesures de Planck Collaboration et al. (2020). Il y a donc un désaccord entre les mesures réalisées sur le CMB (univers jeune, lointain) et les mesures réalisées avec les SNe Ia (univers récent, local). De multiples sources d’erreurs systématiques ont été investiguées mais pour le moment aucune d’elles ne semblent résoudre la tension. Des méthodes de mesure alternatives indépendantes sont aussi mises en oeuvre pour départager les tenants des SNe Ia des tenants du CMB, comme par exemple l’utilisation des fusions d’étoiles à neutrons observées en optique et par ondes gravitationnelles. Aussi, des modèles de nouvelle physique sont en compétition pour réconcilier l’univers jeune et l’univers récent(-Olympics : Schöneberg et al. (2022)).
Un capteur bolométrique est capable d’absorber des photons et de mesurer leur énergie peu importe leur longueur d’onde (par exemple en mesurant l’échauffement d’un matériau). A contrario, un capteur photonique basé sur l’effet photoélectrique devient transparent dans les grandes longueurs d’ondes, lorsque l’énergie du photon passe sous le seuil d’émission d’un électron.
Ou en fréquence exprimée en W/m/Hz.
- Sana, H., de Mink, S. E., de Koter, A., Langer, N., Evans, C. J., Gieles, M., Gosset, E., Izzard, R. G., Le Bouquin, J.-B., & Schneider, F. R. N. (2012). Binary interaction dominates the evolution of massive stars. Science (New York, N.Y.), 337(6093), 444–446. 10.1126/science.1223344
- Nomoto, K., Kamiya, Y., & Nakasato, N. (2013). Type Ia Supernova Models and Progenitor Scenarios. Proceedings of the International Astronomical Union, 7(S281), 253–260. 10.1017/S1743921312015165
- Colgate, S. A., & McKee, C. (1969). Early Supernova Luminosity. The Astrophysical Journal, 157, 623. 10.1086/150102
- Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., Gilliland, R. L., Hogan, C. J., Jha, S., Kirshner, R. P., Leibundgut, B., Phillips, M. M., Reiss, D., Schmidt, B. P., Schommer, R. A., Smith, R. C., Spyromilio, J., Stubbs, C., Suntzeff, N. B., & Tonry, J. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal, 116(3), 1009–1038. 10.1086/300499
- Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G., Deustua, S., Fabbro, S., Goobar, A., Groom, D. E., Hook, I. M., Kim, A. G., Kim, M. Y., Lee, J. C., Nunes, N. J., Pain, R., Pennypacker, C. R., Quimby, R., Lidman, C., … Project, T. S. C. (1999). Measurements of Ω and Λ from 42 High-Redshift Supernovae. The Astrophysical Journal, 517(2), 565–586. 10.1086/307221
- Pereira, R., Thomas, R. C., Aldering, G., Antilogus, P., Baltay, C., Benitez-Herrera, S., Bongard, S., Buton, C., Canto, A., Cellier-Holzem, F., Chen, J., Childress, M., Chotard, N., Copin, Y., Fakhouri, H. K., Fink, M., Fouchez, D., Gangler, E., Guy, J., … Wu, C. (2013). Spectrophotometric time series of SN 2011fe from the Nearby Supernova Factory. Astronomy & Astrophysics, 554, A27. 10.1051/0004-6361/201221008
- Bessell, M. S. (2005). Standard Photometric Systems [Journal Article]. Annual Review of Astronomy and Astrophysics, 43(Volume 43, 2005), 293–336. https://doi.org/10.1146/annurev.astro.41.082801.100251
- Johnson, H. L., & Morgan, W. W. (1953). Fundamental stellar photometry for standards of spectral type on the revised system of the Yerkes spectral atlas. The Astrophysical Journal, 117, 313. 10.1086/145697
- Guy, J., Astier, P., Baumont, S., Hardin, D., Pain, R., Regnault, N., Basa, S., Carlberg, R. G., Conley, A., Fabbro, S., Fouchez, D., Hook, I. M., Howell, D. A., Perrett, K., Pritchet, C. J., Rich, J., Sullivan, M., Antilogus, P., Aubourg, E., … Ruhlmann-Kleider, V. (2007). SALT2: using distant supernovae to improve the use of type Ia supernovae as distance indicators. Astronomy and Astrophysics, 466(1), 11–21. 10.1051/0004-6361:20066930
- Condon, J. J., & Matthews, A. M. (2018). ΛCDM Cosmology for Astronomers. Publications of the Astronomical Society of the Pacific, 130(989), 073001. 10.1088/1538-3873/aac1b2
- Hogg, D. W., Baldry, I. K., Blanton, M. R., & Eisenstein, D. J. (2002). The K correction.
- Betoule, M., Kessler, R., Guy, J., Mosher, J., Hardin, D., Biswas, R., Astier, P., El-Hage, P., Konig, M., Kuhlmann, S., Marriner, J., Pain, R., Regnault, N., Balland, C., Bassett, B. A., Brown, P. J., Campbell, H., Carlberg, R. G., Cellier-Holzem, F., … Wheeler, C. J. (2014). Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. 30. http://arxiv.org/abs/1401.4064
- Hayes, D. S., Latham, D. W., & Hayes, S. H. (1975). Measurements of the monochromatic flux from VEGA in the near-infrared. The Astrophysical Journal, 197, 587. 10.1086/153547
- Souverin, T., Neveu, J., Betoule, M., Bongard, S., Blanc, P. E., Tanugi, J. C., Dagoret-Campagne, S., Feinstein, F., Ferrari, M., Hazenberg, F., Juramy, C., Guillou, L. L., Van Suu, A. L., Moniez, M., Nuss, E., Plez, B., Regnault, N., Sepulveda, E., & Sommer, K. (2024). How the StarDICE photometric calibration of standard stars can improve cosmological constraints? arXiv. 10.48550/ARXIV.2411.03256
- Bohlin, R. C., Gordon, K. D., & Tremblay, P.-E. (2014). Techniques and Review of Absolute Flux Calibration from the Ultraviolet to the Mid-Infrared. Publications of the Astronomical Society of the Pacific, 000–000. 10.1086/677655