L’expansion de l’Univers est aujourd’hui bien décrite par le modèle CDM plat (). Les proportions de chacune de ses composantes sont aujourd’hui évaluées à Planck Collaboration et al. (2020):
Dans ce chapitre, nous allons étudier l’histoire thermique de l’Univers ainsi que l’évolution de sa composition. Jusqu’à maintenant dans ce cours, la matière non-relativiste était traitée comme une seule entité, ralentissant l’expansion de l’Univers par son interaction gravitationnelle. Mais pour étudier son évolution avec la température et ses interactions avec les autres composantes, il faut séparer celles-ci en deux contributions: la matière sombre et la matière baryonique[1] . En effet, en 1933, en étudiant l’amas de Coma, l’astrophysicien Fred Zwicky montre que la masse déduite du mouvement des sept galaxies qui le composent est 400 fois plus grande que la masse déduite du comptage des objets lumineux. Cette mesure est répétée en 1936 sur l’amas de la Vierge et donne cette fois un facteur 200. Ces mesures toutefois un peu imprécises tombent dans l’oubli jusque dans les années 1970, lorsque l’astronome Vera Rubin constate que la vitesse de rotation des étoiles de la Galaxie d’Andromède est bien plus élevée que ne le suggère sa masse lumineuse observée Rubin & Ford, W. Kent, 1970. Le constat est vite répété sur de nombreuses galaxies: une partie de la matière constituant la galaxie est donc une matière sombre, échappant alors à toute détection, représentant souvent la majorité de la masse totale des galaxies. La présence de matière sombre abondante est même visible dans l’amplitude des anisotropies de températures du fond diffus cosmologique (voir fin de chapitre). Aujourd’hui, on estime que la proportion de ces deux formes de matière froide est Planck Collaboration et al., 2020:
.
1Description de l’Univers primordial¶
Le fond diffus cosmologique¶
Si l’Univers est aujourd’hui en expansion, alors il était plus petit dans le passé. L’expansion cosmique réduit la quantité de mouvement des particules d’un facteur et la densité des particules d’un autre . Dans les premiers temps, l’Univers était donc un état chaud et dense. Il doit donc y avoir eu un moment où l’Univers était suffisamment chaud pour que les atomes soient ionisés, et donc dans un état de plasma où les photons interagissent avec les électrons libres. Par ces interactions fréquentes, si l’équilibre thermodynamique est atteint le rayonnement suit un spectre de corps noir défini par la température du milieu (wiki:Planck’s_law). Lors de la transition de l’état plasma à l’état neutre, vers pour un gaz d’hydrogène, l’Univers devient subitement transparent et les photons se propagent librement. Ce rayonnement de corps noir à haute température a été libéré à cet instant. Ce rayonnement dit fossile a été refroidi par l’expansion de l’Univers. Ce fond diffus cosmologique micro-onde a été prédit en 1948 par Ralph Alpher, Robert Herman Alpher & Herman, 1948 et George Gamow Gamow, 1948 autour de , et découvert fortuitement par Arno Penzias et Robert Wilson en 1964 Penzias & Wilson, 1965Penzias & Wilson, 1965 à une température de (Figure 1).

Figure 1:L’antenne cornet Holmdel de 15 mètres des Bell Telephone Laboratories à Holmdel, avec Arno Penzias et Robert Wilson, qui a permis la découverte du CMB. Elle a été construite en 1959 dans le cadre d’un travail sur les satellites de communication pour la NASA ECHO I (By NASA, restored by Bammesk).
Le spectre du fond diffus cosmologique a été caractérisé grâce au satellite COBE, et sa température est aujourd’hui établie à (Fixsen (2009)):
en modélisant ses données par la loi de rayonnement de Planck :
C’est le meilleur rayonnement de corps noir jamais détecté (Figure 2). Comme nous le justifierons plus loin, si les photons interagissent peu avec la matière, alors on démontre que la distribution d’énergie des photons dans le passé est encore un spectre de corps noir, à la température Condon & Matthews, 2018. Donc si on remonte dans le temps jusqu’à la dernière interaction des photons avec la matière, alors à ce moment-là l’Univers était dans un état plus chaud qu’aujourd’hui et à l’équilibre thermique, puisque le rayonnement suivait la loi de Planck. Le rayonnement de fonds diffus cosmologique (CMB) est probablement la preuve la plus directe que l’Univers a bien été sous forme d’un plasma chaud et dense à l’équilibre dans un passé lointain.
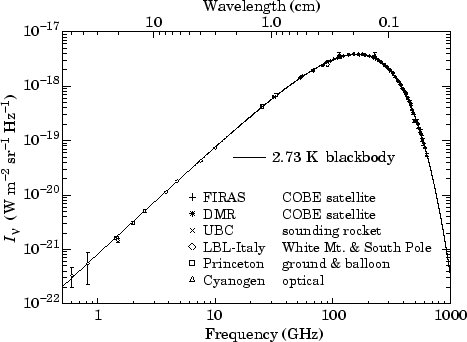
Figure 2:Ajustement d’un modèle de corps noir sur les diverses données mesurant le flux venant du fond diffus cosmologique Mather et al., 1999.
Démonstration de la conservation de la loi de Planck avec le redshift
Figure 3:Notations pour le calcul de l’évolution de la loi de Planck avec le redshift.
La luminance énergétique (Radiance) s’exprime en . Avec les définitions de la distance de luminosité et de la distance angulaire, on montre qu’elle évolue en . En effet, avec les notations de Figure 3, pour une source de luminosité de taille , observée sous un angle solide , dans l’approximation des petits angles :
avec la luminance s’il n’y avait pas d’expansion de l’espace.
La luminance spectrale observée s’exprime en . Tous les photons reçus dans un petit intervalle autour d’une fréquence ont été émis dans un intervalle autour d’une fréquence . La luminance reçue est donc :
On en déduit l’évolution de la luminance spectrale :
Donc le rayonnement de corps noir évolue avec le redshift ainsi :
Un spectre de corps noir reste un spectre de corps noir malgré l’expansion de l’Univers mais à une température d’équilibre :
L’Univers à redshift ¶
Remontons bien au-delà du redshift de la dernière surface de diffusion, et considérons l’Univers à, disons, . Que pouvons-nous en dire ?
Température¶
Pour un gaz de photons, nous savons que :
Or, à l’équilibre thermique, la densité d’énergie d’un gaz de photons est l’intégrale de la loi de Planck :
ave la constante de Stefan-Boltzmann. La température d’équilibre des photons évolue donc comme suit :
La température des photons peut donc être utilisée comme paramètre temporel comme ou si est isotrope.
A redshift 104, la température des photons est donc de l’ordre de K. Les atomes d’hydrogène (majoritaires dans l’Univers) sont donc forcément dans un état ionisé, donc l’Univers est un plasma.
Évolution de avec le redshift
Grâce aux quelques interactions entre les photons du CMB et la matière à différents redshifts, les cosmologistes sont capables de mesurer l’évolution de la température de ce bain de photons ambiant avec l’expansion. Par exemple, on peut regarder l’interaction Compton des photons du CMB avec le plasma d’électrons chauds () situé dans les amas de galaxies (effet Sunyaev-Zeldovich thermique wiki:Sunyaev–Zeldovich_effect). On peut également mesurer le chauffage des molécules CO ou CN du gaz interstellaire par les photons du CMB à différents redshifts. Une des meilleures mesures de la décroissance de la température des photons avec l’expansion est avec (Hurier et al. (2014), voir aussi Noterdaeme et al. (2011)).
Figure 4:Evolution de la température des photons du CMB en fonction du redshift, tiré de Hurier et al. (2014). Le point vert correspond à la mesure de COBE. Les points rouges sont issus de l’émission tSZ des amas de galaxies du catalogue du satellite Planck. Les points bleus sont issus de l’étude de l’absorption par le milieu interstellaire.
Solution to Exercise 1
Densités¶
Nous pouvons maintenant calculer la contribution actuelle des photons du CMB à la densité critique de l’univers en utilisant la température du corps noir :
C’est donc une densité d’énergie négligeable comparée à la matière froide et à l’énergie sombre. Certes, d’autres particules ultra-relativistes telles que les neutrinos contribuent à la partie restante de . Mais avec 3 neutrinos sans masse, on aboutirait seulement à comme on pourra le voir en fin de chapitre.
On définit l’équivalence le moment où matière relativiste et non relativiste sont en proportion égale. Calculons le redshift au moment où les proportions de matière et de rayonnement sont égales :
On en déduit que :
Donc à , le contenu de l’Univers est dominé par la matière relativiste.
Photons¶
Concentrons-nous maintenant sur les propriétés des photons. Nous savons que , donc à leur température est :
D’après la loi de Wien, la fréquence pour laquelle la densité spectrale de Planck est maximum, évolue linéairement avec la température : . Donc, l’énergie caractérisque des photons à est :
Par analyze dimensionnelle et à des facteurs numériques près que nous verrons plus loin, la densité des photons à un redshift vaut :
Baryons¶
Évaluons maintenant la densité de baryons (particules avec 3 quarks comme les protons et neutrons) à . La densité de baryons est aujourd’hui . Avec une densité critique de , cela donne environ :
L’univers est donc largement dominé par les photons en terme de densité de particules, et cette proportion reste remarquablement constante tout le long de l’histoire de l’Univers :
Taux d’expansion¶
La valeur du taux d’expansion de Hubble peut être déduite de l’équation de Friedmann :
Prenons les valeurs canoniques , et pour la densité de matière relativiste (photons et neutrinos). A , cela donne :
L’expansion de l’Univers était beaucoup plus rapide qu’aujourd’hui !
Libre parcours moyen des photons¶
Enfin, on peut s’interroger sur le libre parcours moyen des photons. Les photons interagissent préférentiellement avec les électrons par diffusion Thomson , car la diffusion sur les protons est atténuée par un facteur . Une bonne approximation du libre parcours moyen des photons est donnée par :
où est la section efficace de diffusion de Thomson (). Pour la densité électronique, considérons que l’Univers étant neutre, il y a un électron pour chaque proton donc . Le temps typique entre deux interactions est alors :
aujourd’hui si la matière est dans un état ionisé, et à l’époque :
On voit donc que dans le passé les interactions entre matière et photons étaient suffisamment fréquentes pour atteindre l’équilibre thermique en un temps court devant l’expansion de l’Univers. On peut donc ainsi justifier que lors de leurs dernières interactions avec la matière les photons suivaient la loi de Planck. Mais, depuis, ces photons n’interagissent plus avec elle. Les photons du CMB ne sont donc pas en équilibre thermique avec quoi que ce soit d’autre aujourd’hui. Non seulement le taux d’interaction est faible, mais on compte 109 photons pour un baryon. L’immense majorité des photons du CMB n’ont donc jamais été en contact avec des particules depuis leur émission, donc leur spectre suit toujours la loi du corps noir (5). De plus, en raison de leur nombre il est légitime d’assimiler la température de l’Univers à celle des photons, ce que l’on fera souvent par la suite.
Scénario du Big Bang¶
L’Univers à était beaucoup plus chaud et plus dense. A cette température, les atomes sont ionisés et on a donc un plasma. Tout comme aujourd’hui, la densité du nombre de photons était significativement plus grande que celle des baryons. Enfin, les interactions entre photons et particules chargées étaient beaucoup plus fréquentes (plusieurs par temps de Hubble), il est donc tout à fait logique de considérer l’Univers comme un plasma en équilibre thermique.
A partir de cette description, nous pouvons esquisser un scénario d’évolution du plasma primordial en cataloguant les différents phénomènes physiques qui peuvent se produire lorsque celui-ci se refroidit. En voici un résumé non exhaustif.
2Thermodynamique statistique à l’équilibre¶
Nous allons maintenant aborder une description plus fine de ce qu’il s’est passé dans l’Univers primordial en utilisant la physique statistique.
Description statistique¶
Modélisons le contenu de l’Univers comme un gaz de particules interagissant faiblement. Nous pouvons alors utiliser le formalisme de la physique statistique et décrire le gaz par les positions et les impulsions de toutes ses particules, définies sur l’espace des phases .
Dans un gaz de particules à l’équilibre thermodynamique, le nombre de particules pouvant occuper un état d’énergie suit une fonction de distribution statistique . En cosmologie, en raison de l’homogénéité de l’Univers, ne peut pas dépendre de la position . De plus, en raison de l’isotropie, ne peut dépendre que de la norme de la quantité de mouvement et non de sa direction.
Muni des fonctions de distribution, nous pouvons en déduire des propriétés macroscopiques du gaz en évaluant la probabilité d’occupation des états du système. Mais quelles sont-elles ? Tout d’abord, la mécanique quantique nous impose que la densité des états dans l’espace des phases est finie. En effet, considérons une boîte de taille , avec des conditions périodiques et résolvons l’équation de Schrödinger, nous obtenons que les valeurs possibles de la quantité de mouvement sont :
où et sont les vecteurs unitaires et est la constante de Planck. En conséquence, dans l’espace des quantités de mouvement, il y a un état par cube élémentaire de volume . La densité d’états dans l’espace des quantités de mouvement est donc . Ensuite, il n’y a qu’une particule dans la boite quantique donc un seul état de position : la densité d’états dans l’espace des positions est de . Au total, si la particule possède degrés de liberté internes, la densité d’états dans l’espace des phases est :
La densité d’états est donc indépendante du volume . Elle reste la même pour un système arbitrairement grand.
Les propriétés macroscopiques (densité de nombre, densité d’énergie, pression) se déduisent de la probabilité d’occupation des états et de la densité d’états de l’espace des phases. La densité volumique de particules d’impulsion comprise entre et est par exemple donné par :
La densité volumique particulaire moyenne du gaz est:
Pour la densité d’énergie moyenne, puisqu’on considère que les particules interagissent faiblement et ne sont pas confinées, alors les niveaux d’énergie sont ceux d’une particule libre . Pour obtenir la densité d’énergie du gaz, il suffit de faire la somme des niveaux d’énergie pondérés par leur probabilité d’occupation :
Nous pouvons obtenir de la même manière la pression cinétique du gaz :
Au final, le tenseur énergie-impulsion pour un ensemble de particules quantiques peut s’écrire :
Remarquons que cette formule est la version quantique en limite continue de la formule (4) obtenu pour un gaz parfait classique, avec la convention d’unités .
L’équilibre cinétique¶
Lorsque les particules peuvent échanger souvent de l’énergie et de la quantité de mouvement par des collisions élastiques, le gaz atteint un état d’entropie maximale, appelé équilibre cinétique. Les fonctions de distribution peuvent être obtenues en évaluant l’entropie du gaz () et en la maximisant, pour une énergie totale donnée et un nombre total de particules donné.
Selon la nature fermionique ou bosonique des particules du gaz, la combinatoire donnant les probabilités d’occupation de l’ensemble des micro-états est différente à cause du principe d’exclusion de Pauli. A énergie totale et nombre total de particules fixés, après usage des multiplicateurs de Lagrange, ces contraintes imposent que les fonctions de distribution à l’équilibre thermodynamique sont :
avec la température du gaz, le potentiel chimique de l’espèce et son nombre de degrés de liberté internes (par exemple le nombre d’états de spin). Elles donnent le nombre de particules pouvant occuper un état d’énergie selon que ce sont des bosons ou des fermions, à l’équilibre thermodynamique.
Dans la limite classique[2], on retrouve la distribution de Maxwell-Boltzmann :
valable pour les fermions et les bosons.
Les fonctions de distribution de Fermi-Dirac et de Bose-Einstein dépendent de deux paramètres : la température du gaz , et le potentiel chimique de l’espèce , qui caractérise la variation d’entropie ou d’énergie lorsque le nombre de particules varie.
Si le gaz contient plusieurs espèces en interaction, chaque espèce est décrite par sa propre fonction de distribution, son propre potentiel chimique , et éventuellement (si elle est découplée) sa propre température . Nous pouvons en déduire la densité particulaire, la densité d’énergie et la température de chaque espèce.
Si toutes les espèces sont en équilibre cinétique, elles partagent la même température : , le système a atteint l’équilibre thermique.
L’équilibre chimique¶
Les variations d’énergie d’un système peuvent être exprimées en fonction de de son entropie, de son volume et de sa température :
ou encore :
Considérons deux systèmes et à des températures et mis en contact. Si les deux systèmes sont isolés, les deux principes de la thermodynamique stipulent :
l’énergie l’énergie totale de () est conservée :
l’entropie de () atteint un maximum :
ce qui donne à l’équilibre.
Considérons maintenant que et peuvent échanger des particules (en gardant le nombre total de particules constant), en passant du premier au second réservoir par exemple. Nous avons :
et l’entropie de atteint un maximum, ce qui donne :
d’où . À l’équilibre, les deux potentiels chimiques sont égaux.
Considérons maintenant le cas d’une réaction chimique entre les particules des deux systèmes :
c’est-à-dire le cas de quatre systèmes , , et mis en contact. En suivant le même même raisonnement, on peut montrer que :
ils atteignent une même température d’équilibre température ;
à l’équilibre, on a .
Si plusieurs espèces interagissent par le biais d’une réaction, par exemple :
et atteignent l’équilibre chimique (c’est-à-dire l’état d’entropie maximale), les potentiels chimiques satisfont la relation stoechiométrique :
en plus de toute équation des lois imposées par la conservation de charge ou matière (nombre de particules, charge électrique, charge baryonique, etc.).
Avancement de réaction
Pour une réaction du type :
à température et volume fixés (donc pendant un temps court devant l’inverse du taux d’expansion de l’Univers), l’énergie libre est simplement :
avec l’avancement de la réaction (+ pour un produit, - pour un réactif). La confition de minimisation du potentiel thermodynamique impose :
avec l’affinité chimique. Comme , deux cas sont possibles :
: la réaction avance dans le sens de la formation des produits et consomamtion des réactifs car il y a plus de potentiel chimique du côté des réactifs que de produits;
: la réaction avance dans le sens de la consommation des produits et formation des réactifs. A l’équilibre chimique, donc neutralisation des potentiels chimiques:
Pour les photons, il n’y a pas de charge conservée. Même le nombre de photons n’est pas conservé. Par exemple, nous avons une double diffusion Compton ou Bremstrahlung . D’où :
Les particules et leurs antiparticules sont de charges opposées, d’où, à l’équilibre :
On peut aussi utiliser la réaction pour arriver à la même conclusion. Puis, dans l’Univers chaud à l’équilibre thermodynamique, on peut montrer que les potentiels chimiques des fermions vérifient du fait de leur équilibre chimique avec leurs antiparticules.
Densité et pression des fermions et bosons¶
Nous avons maintenant tout ce qu’il faut pour calculer la densité particulaire, la densité d’énergie et la pression des constituants de l’Univers. Les potentiels chimiques peuvent être négligés à haute température (), et les équations (27), (28) et (29) peuvent être réécrites :
avec le signe pour les fermions et le signe pour les bosons.
Dans le cas général, les intégrales ci-dessus doivent être calculées numériquement. Il existe cependant deux limites intéressantes, qui permettent de comprendre les processus physiques en cours : le cas où les particules sont relativistes () et le cas opposé des espèces non relativistes ().
Avant de poursuivre, définissons : , et .
Limite relativiste¶
A très haute température, les fermions sont en équilibre avec leurs anti-particules, donc on a approximativement la même densité pour les deux entités. Puisque , en regardant droit dans les yeux l’expression pour la densité particulaire sachant que , la seule façon pour que les deux intégrales soient égales avec des potentiels chimiques de signe opposé est qu’ils soient nuls. Donc dans l’Univers primordial, pour les fermions[3] relativistes . Avec , nous pouvons alors réécrire et comme :
Dans la limite relativiste, nous avons et les intégrales et peuvent être calculées exactement :
avec la fonction de Riemann. Nous trouvons :
On voit que les densités particulaires et d’énergie sont identiques pour les bosons et fermions relativistes à un facteur numérique près. De plus, les photons sont des bosons avec polarisations possibles, donc on a ici redémontré la loi de Stefan-Boltzmann.
Concernant le calcul de la pression, on a pour les particules relativistes, donc :
On retrouve l’équation d’état déjà introduite précédemment.
Calculs de et
Pour calculer , il est utile de connaître la définition de la fonction zeta de Riemann :
Pour les bosons, nous obtenons immédiatement :
Pour les fermions, nous avons :
L’intégrale peut aussi être exprimée comme une fonction de . Pour les bosons, on obtient immédiatement
Pour les fermions, nous utilisons la même astuce que ci-dessus, et nous obtenons :
Limite non relativiste¶
Dans la limite non relativiste , l’énergie des particules est égale à leur masse au repos (donc ). Le potentiel chimique n’est plus forcément négligeable non plus si la température baisse trop. Les intégrales et se réduisent à une seule expression si car à de telles basses densités on peut omettre la nature fermionique ou bosonique des particules :
Or et nous pouvons développer : , et nous pouvons approximer l’intégrale ci-dessus avec :
Ainsi, pour les fermions et les bosons, nous obtenons après quelques calculs :
Lorsque la température descend en dessous de la masse au repos des particules, la densité du nombre de particules chute exponentiellement selon une loi de Bolztmann. La densité d’énergie et la pression sont (au premier ordre) proportionnelles à et diminuent en conséquence. Elles suivent d’ailleurs les lois attendues de la physique non relativiste (loi du gaz parfait (Ideal gas) et énergie interne volumique ). Les espèces non relativistes se comportent donc comme un gaz sans pression (car i.e. ). C’est cette description de la matière non relativiste que nous avons utilisée pour calculer l’expansion dans un univers dominé par la matière non relativiste.
Ordre de grandeur des potentiels chimiques des fermions
Pour les fermions, montrons que leur potentiels chimiques sont négligeables. Comparons les densités particulaires avant et après l’annihilation de particules avec leurs antiparticules (voir Kolb & Turner, 1990 p.89):
Or pour les baryons, aujourd’hui leur densité particulaire est . Dans le cas relativiste, on a donc donc le potentiel chimique des baryons est bien négligeable. Pour les électrons, comme l’Univers est électriquement neutre[4], alors on a le même ordre de grandeur. Concernant les neutrinos, c’est plus ambigü car le fond diffus de neutrinos n’a pas encore été détecté, mais en première approximation on peut penser que là encore le potentiel chimique doit être négligeable (Weinberg (1989) p.531).
Nombre effectif d’espèces relativistes¶
Définition¶
Nous partons d’un plasma primordial en équilibre thermique et chimique, contenant des espèces à la température . Avant l’équivalence, le taux d’expansion est une fonction directe de la densité massique de matière relativiste :
où est la somme des densités de chaque espèce relativiste présente dans le fluide primordial :
Nous avons vu dans la section précédente que tant que la particule reste relativiste, alors que la densité chute exponentiellement quand la température tombe en dessous de la masse de la particule. La densité de l’Univers est donc dominée par celle des particules relativistes à haute température. Plus précisément, nous pouvons écrire :
On définit le nombre effectif de degrés de liberté relativistes du plasma à la température :
Lorsque l’espèce est encore à l’équilibre thermique avec les photons, alors . Lorsque la température descend en dessous de la masse de l’une des espèces, elle devient relativiste et disparaît de la somme ci-dessus. Si elle se découple des photons avec une température différente des photons, tout en restant relativiste, alors elle reste présente dans avec un poids .
Évolution de ¶
Figure 5:Caractéristiques des particules du modèle standard pour calculer . En l’absence de neutrinos droits, on ne compte qu’un état de spin pour les neutrinos. Les gluons pouvant porter 2 charges de couleurs de l’interaction forte parmi , cela fait 9 états possibles mais la combinaison linéaire de couleur blanche retire un degré de liberté à l’interaction forte donc il n’y a finalement que 8 états indépendants (Gluon).
Etudions maintenant l’évolution de , qui raconte simplement l’évolution de la matière relativiste du plasma primordial au fur et à mesure qu’il se refroidit avec l’expansion. Commençons autour de GeV. Toutes les particules du modèle standard sont relativistes (voir Figure 5). Lorsque toutes les particules sont relativistes, le nombre total de degrés de liberté est de :
pour les fermions, et
pour les bosons, ce qui donne
Pour voir ce qui va se passer ensuite, il suffit de regarder les masses des particules énumérées dans le Figure 5. Le quark top s’annihile en premier car c’est la particule la plus lourde. Pour , le plasma à l’équilibre ne peut plus produire de quarks top par annihilation de paires d’autres particules, réduisant le nombre de degrés de liberté à :
Puis, nous avons donc le boson de Higgs, suivi des bosons électrofaibles et : ce qui réduit à 86.25. Ensuite, et s’annihilent, et est alors réduit à 61.75.
L’événement suivant est la transition de phase QCD, qui se produit à . Les quarks se combinent en hadrons[1] (protons, neutrons et mésons). A cette température, tous sont non relativistes sauf les pions. A ce stade, les seules espèces relativistes restantes sont les photons, les neutrinos, les électrons et les muons et les 3 pions de spin 0 (avec donc degrés de liberté internes). On en déduit le nombre de degrés de liberté relativistes restant :
Ensuite, les pions et les muons s’annihilent, ce qui donne :
Les deux événements significatifs suivants sont le découplage des neutrinos autour de puis l’annihilation des électrons et des positrons ().
Entropie¶
Conservation de l’entropie¶
L’entropie de l’Univers est une fonction des variables extensives énergie interne , volume et des nombres de particules d’une espèce . La variation d’entropie d’un volume comobile de plasma à l’équilibre thermodynamique obéit au seconde principe de la thermodynamique :
Pour un volume d’Univers suffisamment grand pour être considéré homogène et isotrope, l’entropie ne peut qu’augmenter ou rester constante. De plus, les potentiels chimiques des espèces dominantes (relativistes) sont négligeables dans le plasma primordial (). Or, à l’équilibre thermodynamique on a :
où pression et densité d’énergie ne sont finalement que des fonctions de la température d’équilibre, que les espèces soient relativistes ou non (voir formules précédentes). Dès lors, la variation d’entropie est une fonction du volume et de la température avec (Weinberg (1989) p.532):
On identifie les dérivées partielles :
et grâce aux relations de Maxwell (ou théorème de Schwartz), on a :
Avec cette dernière relation, on peut terminer le calcul de la variation d’entropie :
Si on considère une variation par rapport au temps :
et enfin en se souvenant de la relation de conservation de l’énergie ,
L’entropie dans un volume comobile est donc conservée et s’écrit[5] :
On définit l’entropie volumique, fonction de la température uniquement :
Entropie du plasma primordial¶
Pour les espèces relativistes, comme , nous obtenons les entropies volumiques :
Pour une collection d’espèces (fermions et bosons) à l’équilibre aux températures , nous avons :
avec
Puisque l’entropie est conservée, alors :
Température de l’Univers¶
Maintenant que nous avons une relation de conservation, on peut établir un lien entre l’expansion de l’Univers et sa température d’équilibre :
Cette relation donne une relation entre température et facteur d’échelle à tout instant dans l’histoire de l’Univers. Elle varie bien avec le redshift en mais avec un facteur de proportionnalité qui change par seuil selon la composition de l’Univers (Figure 7).
Figure 7:Evolution de la température au cours de l’expansion de l’Univers selon les espèces relativistes présentes (équation (90)). En réalité les transitions de phase ne sont pas soudaines, donc la courbe réelle doit être lissée.
Expansion du plasma primordial¶
La loi d’expansion obéit à la première équation de Friedmann :
et donc :
Ainsi, aux variations près du nombre effectif de degrés de liberté dans le plasma primordial. Gardez cela à l’esprit, cela sera utile pour comparer le taux d’expansion avec les divers taux de réaction entre les différentes espèces.
En injectant l’évolution de la température avec le facteur d’échelle (équation (90)), on retrouve que dans l’Univers primordial (équation (2)) avec le facteur de proportionalité qui change quand varie. Mais le taux d’expansion vaut alors simplement ce qui donne :
Ainsi, à la température de , comme alors , il s’est écoulé s depuis le début de l’Univers.
3Histoire de la matière dans l’Univers primordial¶
Nous avons maintenant (presque) tout ce dont nous avons besoin pour discuter de l’évolution de la matière dans le plasma primordial. Lorsque la température est suffisamment élevée, le plasma primordial contient toutes les particules du modèle standard, sous forme relativiste (plus toutes les particules qui n’ont pas encore été découvertes, par exemple les particules hypothétiques qui constitueraient la matière sombre froide aujourd’hui). Toutes les espèces de particules sont en équilibre thermodynamique (cinétique et chimique, même température ). Mais au fur et à mesure de l’expansion de l’Univers, la température diminue au rythme du taux d’expansion. L’une après l’autre, les différentes espèces massives deviennent non relativistes, s’anéantissent, et leurs densités d’énergie deviennent sous-dominantes par rapport aux espèces relativistes.
Si l’Univers était en parfait équilibre thermodynamique, et si cet équilibre avait persisté jusqu’à aujourd’hui, les abondances observées de particules massives seraient bien inférieures à ce qu’elles sont, puisque chaque espèce massive voit sa densité exponentiellement supprimée lorsqu’elle devient non relativiste. En fait, les équilibres thermiques et chimiques ont besoin de taux de collision (et/ou de réaction) fréquents pour être maintenus. Avec l’expansion de l’Univers, les particules se diluent, ce qui rend plus difficile le maintien des taux de réaction.
Puisque (93), le taux de variation de la température est le taux de Hubble :
Pour pouvoir considérer que le système est à l’équilibre thermodynamique, il faut qu’il y ait suffisamment d’interactions dans un temps plus court que le temps de variation de la température. La règle empirique est donc qu’il faut au moins plusieurs interactions par temps de Hubble pour pouvoir maintenir l’équilibre thermique et chimique. Ainsi, si on note le taux d’interaction, l’équilibre thermique et chimique est maintenu si . Lorsque le taux de réaction chute en dessous de , l’équilibre thermodynamique n’est plus maintenu, les densités de particules sont gelées à leurs valeurs d’avant le découplage. Le gel des interactions est un mécanisme essentiel pour expliquer l’abondance actuelle des particules.
Découplage des neutrinos et annihilation électron-positron¶
Le découplage des neutrinos est notre première illustration de l’effet de gel. Les neutrinos n’interagissent que par le biais de l’interaction faible. Autour de , ils sont encore thermalisés avec le bain de photons par des interactions telles que :
A ces énergies, la section efficace de l’interaction faible est avec la constante de couplage de Fermi ParticleDataGroup et al., 2022. Par conséquent, le taux d’interaction diminue beaucoup plus rapidement que le paramètre de Hubble :
Autour de , et les interactions entre les neutrinos et les autres particules du modèle standard deviennent improbables. Les neutrinos se découplent du plasma primordial mais restent relativistes (). Même s’ils n’interagissent plus avec d’autres particules, ils conservent dans une excellente approximation leur fonction de distribution de Fermi-Dirac (voir encadré) avec une température qui n’est affectée que par le décalage vers le rouge. Ainsi, à ce stade :
tant que l’évolution de la température des photons ne varie pas.
Le spectre des espèces découplées sans interaction
Pour les espèces ultra-relativistes, nous avons . Le nombre de particules à dans le volume de l’espace des phases est :
A , un peu plus tard, les mêmes particules se trouvent dans le volume de l’espace des phases . Les impulsions évoluent en et le volume comme . On peut donc écrire :
avec et . Le spectre de particules ultra-relativistes reste donc inchangée avec l’expansion, si ce n’est sa température moyenne.
Annihilation et température du fond diffus de neutrinos¶
Mais peu après le découplage des neutrinos, lorsque environ s après le Big Bang, les électrons et les positrons s’annihilent :
ce qui va produire suffisamment d’énergie et d’entropie pour chauffer le gaz de photons et mener à une différence entre la température des photons et ceux des neutrinos découplés . L’entropie étant conservée, nous avons avant l’annihilation :
après annihilation :
En écrivant la conservation de l’entropie, nous avons :
Or on a donc :
Pour les neutrinos découplés, donc finalement :
Nous constatons donc qu’après l’annihilation , la température du fond cosmique de neutrinos est effectivement inférieure à la température du CMB. Aujourd’hui, en utilisant , nous trouvons :
Le rapport entre les températures des photons et des neutrinos se retrouve sur la Figure 8 obtenue après un calcul précis de l’évolution du milieu pendant l’annihilation .
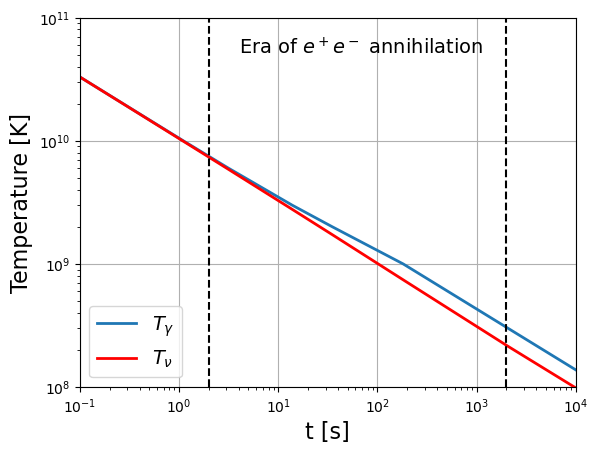
Figure 8:Evolution de la température des photons et des neutrinos au cours de l’annihilation (figure adaptée de Weinberg (1989) p. 529,540 et originellement de Peebles (1966)).
Nous pouvons en déduire la densité de neutrinos en fonction de . Les neutrinos sont des fermions avec 3 saveurs donc si on les suppose sans masse, aujourd’hui leur densité serait :
ce qui donne par saveur ( au total). Pour la densité d’énergie du fond de neutrinos, nous trouvons :
et numériquement, on trouve . On en déduit la proportion totale de matière relativiste dans l’Univers (si les neutrinos le sont) :
Le découplage des neutrinos s’est légèrement superposé à l’annihilation de . Comme les neutrinos interagissaient encore au moment de l’annihilation, le bruit de fond des neutrinos a été légèrement affecté par l’énergie et l’entropie libérées par l’annihilation de . Dans la littérature, cela est pris en compte en introduisant un nombre effectif de neutrinos , évaluer numériquement à 3.046. En tenant compte de cela, le nombre de neutrinos et la densité d’énergie sont :
Enfin, les valeurs correctes et après l’annihilation sont :
En réalité, les neutrinos ont des masses, avec deux conséquences importantes (1) nous ne savons pas s’ils sont encore relativistes aujourd’hui (toutes saveurs confondues) (2) est plus grand que la valeur citée ci-dessus. Les expériences observant les oscillations de neutrinos imposent que la somme des masses des neutrinos, notée est supérieure à donc au moins une saveur de neutrino serait non relativiste aujourd’hui si on compare à . Du point de vue de la cosmologie, si on impose de façon très prudente que alors on aboutit à une contrainte , et les relevés cosmologiques regardant l’effondrement gravitationnel des grandes structures de l’Univers imposent (DESI Collaboration et al. (2024)).
Big Bang Nucleosynthesis (BBN)¶
Revenons environ ms après le Big Bang lorsque le température de l’Univers est de quelques dizaines de MeV. L’Univers est alors essentiellement un plasma chaud à l’équilibre thermodynamique de baryons, de photons, d’électrons, de positrons et de neutrinos (sur le point de se découpler des autres particules). On rappelle que le rapport baryon sur photon est une constante (18) et vaut plus précisément :
avec la mesure de sur le spectre de puissance des anisotropies de température du CMB Planck Collaboration et al. (2020). L’Univers continuant son expansion, il se refroidit et les protons et neutrons peuvent fusionner pour former les premiers noyaux atomiques. C’est ce qu’on appelle la nucléosynthèse primordiale (BBN).
Rapport neutron sur proton¶
Le taux de formation de ces noyaux va dépendre d’un paramètre essentiel : le rapport des nombres de neutrons et protons disponibles au moment où la formation des noyaux devient possibles.
A ms, les protons et neutrons sont à l’équilibre thermodynamique l’un avec l’autre via les interactions :
et même celle-ci (moins efficace) :
Tant que ces interactions sont possibles, le rapport neutron sur proton est donné par les densités particulaires à l’équilibre (55) pour des particules non-relativistes[6] :
Or . De plus, d’après la première réaction, à l’équilibre chimique on a , donc on peut supposer que si les potentiels chimiques des électrons et neutrinos sont négligeables. On en déduit que le rapport neutron sur proton se simplifie en :
Par conséquent, tant que la température est telle que , alors il y a autant de neutrons que de protons dans l’Univers. Mais en deçà de , la proportion de neutrons chute exponentiellement. Posons le rapport neutron sur baryon si les espèces sont à l’équilibre à la température . Alors :
Donc la densité de neutrons devrait être quasi nulle aujourd’hui, mais cette équation est valable seulement tant que les réactions ont lieu. En effet, si le taux d’expansion de l’Univers devient comparable ou supérieur au taux d’interaction, alors les réactions s’arrêtent et la proportion est gelée à la valeur atteinte. Le mécanisme de gel des réactions impliquant des particules massives est important en cosmologie pour comprendre l’abondance des particules massives aujourd’hui.
Pour la réaction , le taux d’interaction est donné par (Kolb & Turner (1990) p.90, Weinberg (1989) p.547 et originellement dans Peebles (1966)) :
avec les distributions de Fermi-Dirac des particules et :
avec la constante de Fermi et le couplage axial-vecteur des nucléons (Kolb & Turner (1990) p.91). Malheureusement, les 6 intégrales donnant les taux des 6 réactions doivent être calculées numériquement, car on va voir que la proportion de neutron gèle à une température proche de et , ce qui empêche de faire des approximations brutales pour se concentrer sur un régime de haute ou basse énergie.
Approximation numérique des intégrales
Une approximation numérique de la somme des intégrales pour les deux taux d’interaction des réactions (117) est Bernstein et al. (1989) :
Ensuite, pour obtenir l’évolution de la densité de neutrons, une méthode d’intégration numérique est proposée dans Dodelson (2003) p.67 en définissant la proportion de neutron :
Pour déterminer la température de gel du rapport , il faut comparer les taux de réaction au taux d’expansion . Posons le taux cumulé des 3 interactions formant des neutrons, et la somme des autres réactions formant des protons. Après intégration numérique, on observe Figure 9 que décroit en fonction de la température et converge vers un plateau correspondant à l’inverse du temps de demi vie du neutron (indépendant de l’expansion). Il est supérieur au taux donc c’est celui-qui compte dans le mécanisme de gel. Le taux est comparable au taux d’expansion à la température :
C’est la température de gel de la proportion de neutrons libres. Elle a lieu seulement après le Big Bang, donc un temps court devant le temps de demie-vie du neutron libre . On note également que , donc aucune approximation raisonnable ne pouvait être réalisée pour calculer les intégrales.
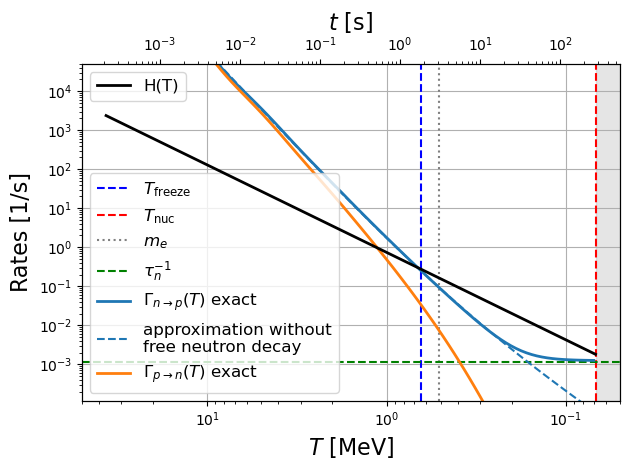
Figure 9:Comparaison des taux de réaction et du taux d’expansion . La température de gel de la densité des neutrons est définie par le croisement des courbes. Le taux de réaction atteint un plateau correspondant au taux de désintégration du neutron, indépendant de l’expansion. La région grisée correspond à la formation des noyaux atomiques: il n’y a plus de neutrons libres à ce stade donc les courbes ne sont plus valables.
Un bilan détaillé de la densité de neutrons permet d’écrire l’équation de Boltzmann suivante :
Le dernier terme des équations correspond à la dilution des particules avec l’expansion si leur nombre est conservé dans un volume comobile. Le nombre total de protons et de neutrons est en revanche conservé dans un volume comobile :
Définissons la proportion de neutrons . La proportion de protons s’en déduit par . L’équation différentielle pour la densité de neutrons se réécrit :
soit :
Étudions maintenant la densité relative de neutrons . Après intégration numérique avec comme condition initiale :
on obtient la Figure 10. Si la désintégration spontanée du neutron est omise (courbe tiretée), la fraction de neutron converge vers , soit :
i.e. 1 neutron pour 6 protons[7].
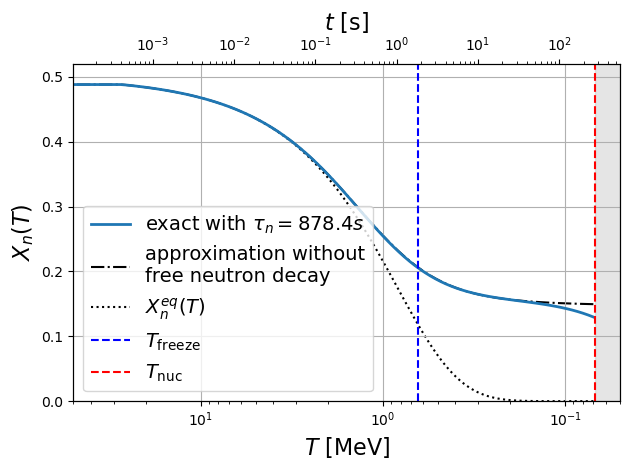
Figure 10:Fraction de neutrons en fonction du temps calculé par l’équation (130) (trait plein). Si la désintégration du neutron est négligée, alors on obtient la courbe en pointillé (). La distribution d’équilibre donne la proportion de neutrons si les réactions ne sont pas gelées par l’expansion de l’Univers.
Si la nucléosynthèse démarre après un temps comparable à , alors cette proportion de neutron sera plus faible à cause de la désintégration spontanée du neutron libre. La question maintenant est de calculer à quelle température les premiers noyaux peuvent se former pour savoir quelle est la fraction de neutrons disponibles à ce moment là, puisqu’une fois confinés dans les noyaux les neutrons sont stables. Comme les interactions à deux particules sont les plus probables, il faut commencer par étudier la température à laquelle le noyau de deutérium peut se former.
Synthèse du deutérium¶
Après la température de gel des neutrons , la proportion de neutrons et de protons est donc stable, à ceci près que les neutrons libres ont une demi-vie d’environ 15 minutes. Toutefois, si la température descend suffisamment, protons et neutrons peuvent se combiner pour former le plus léger des noyaux atomiques par interaction forte, le deutérium , via la réaction :
La question est donc: quand la formation du deutérium a-t-elle lieu et combien y a-t-il de neutrons disponibles à cet instant?
Le deutérium possède une énergie de liaison :
Il est donc plus favorable de former des atomes de deuterium que de garder des protons et des neutrons séparés car . Notons que cette énergie est plus haute que . Pour autant, il faut se rappeler qu’il y a 109 photons pour un baryon et que ces photons suivent une distribution de corps noir: même à des énergies comparables à , il existe encore une pléthore de photons capable de dissocier les noyaux de deutérium nouvellement formés. La température de formation du deutérium dans l’univers primordial doit donc forcément faire intervenir , et aura lieu à une température plus basse de , lorsqu’il n’y aura plus suffisamment de photons de très haute énergie capable de dissocier les noyaux.
Calculons cette température . On définit la température de démarrage de la nucléosynthèse comme celle où la moitié des neutrons ont été consommés pour former du deutérium, c’est-à-dire lorsque . Le rapport des densités de particules à l’équilibre est :
avec (car le deutérium est un boson massif de spin 1), , et (Ryden (2017) p.219).
Le rapport deutérium sur neutron s’écrit :
En supposant que de toute façon le nombre de protons va peu diminuer au cours de la formation du deutérium, on peut estimer que la densité de protons à est environ :
On en déduit alors la température par l’inversion numérique de l’équation suivante, faisant intervenir :
soit s après le Big Bang, avec dorénavant puisque l’Univers possède une température inférieure à . On note que est seulement légèrement plus petit que donc la désintégration spontanée du neutron libre a dû faire baisser la proposotion de neutron disponible après . A , la fraction de neutrons encore présente est environ de :
La désintégration spontanée du neutron est donc notable à cette échelle de temps.
Synthèse de l’hélium 4¶
La formation des noyaux d’hélium n’est possible que via la fusion de noyaux de deutérium :
car il est beaucoup plus improbable que deux protons et deux neutrons se rencontrent par hasard pour former un noyau d’hélium. Or l’énergie de liaison de l’hélium 4 est bien supérieure à celle du deutérium ()[8], donc sa formation est très favorisée. Par conséquent, dès que des noyaux de deutérium sont disponibles, ils sont quasiment immédiatement et totalement fusionnés en noyaux d’hélium 4 et il n’y a déjà plus de photons de haute énergie capable de les dissocier. Presque tous les neutrons disponibles à vont donc terminer dans un noyau d’hélium.
Comme deux neutrons vont dans un noyau d’hélium 4, le nombre maximum de noyaux d’hélium formables est égal à la moitié des neutrons disponibles (qu’ils soient libres ou dans les noyaux de deutérium). On en déduit l’abondance en hélium 4 en nombre de noyaux comme étant :
En terme de masse, l’abondance d’hélium 4 dans l’Univers à la fin de la nucléosynthèse primordiale peut être au maximum de (Figure 11):
le reste étant de l’hydrogène (à en masse). En terme de densités particulaire, on obtient également .
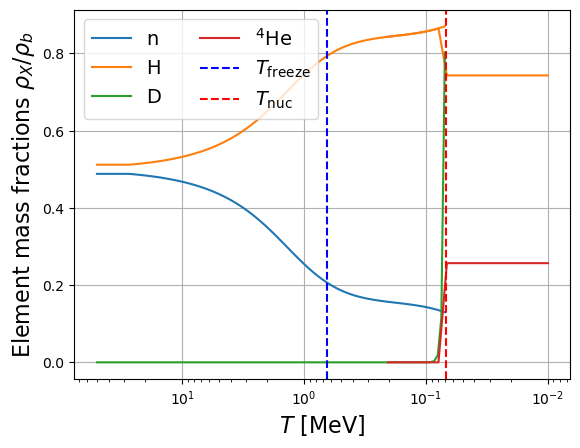
Figure 11:Fraction massique des différentes noyaux légers dans l’Univers au cours du temps, calculée via le modèle simple détaillé dans ce chapitre.
Des calculs plus précis montrent que la synthèse des noyaux atomiques démarre environ 3 minutes après le Big Bang et se termine 20 minutes après. Ils prédisent autour de 24%, car une petite fraction des neutrons demeurent dans d’autres noyaux légers après comme le deutérium, le lithium, etc (Figure 12). Ces prédictions sont en bon accord avec les mesures (voir Figure 13). Avant la découverte des anisotropies de température du CMB dans les années 2000, la comparaison de la mesure des abondances des éléments légers (par l’observation du milieu interstellaire ou des galaxies: bandes grises horizontales de la Figure 13) avec ces prédictions était un moyen de mesurer et donc (voir équation (113)). La mesure de par les anisotropies de température (bande grise verticale de la Figure 13) est plus précise mais en accord avec les prédictions de la BBN ce qui montre la robustesse du modèle standard de la cosmologie (sauf pour le lithium où un désaccord persiste).
Dans tous les cas, avec uniquement le mécanisme stellaire de fusion de l’hydrogène au coeur des étoiles en hélium (et ensuite la fusion de l’hélium en carbone, oxygène, etc), il n’est pas possible d’expliquer une telle abondance de l’hélium dans l’Univers. Seul le passage par un plasma chaud à des centaines de millions de degrés contenant des neutrons libres, même au plus 20 minutes en se refroidissant, permet d’expliquer les d’hélium présents dans l’Univers. C’est donc une preuve importante de l’existence d’un état où l’Univers était un plasma chaud et dense pendant au moins quelques minutes.
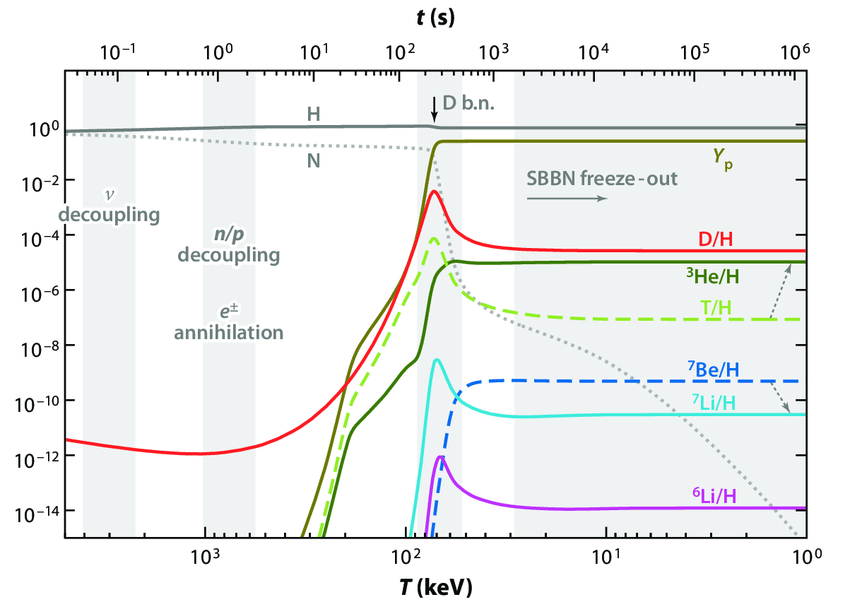
Figure 12:Synthèse des éléments légers dans l’Univers primordial (d’après Pospelov & Pradler (2010)).
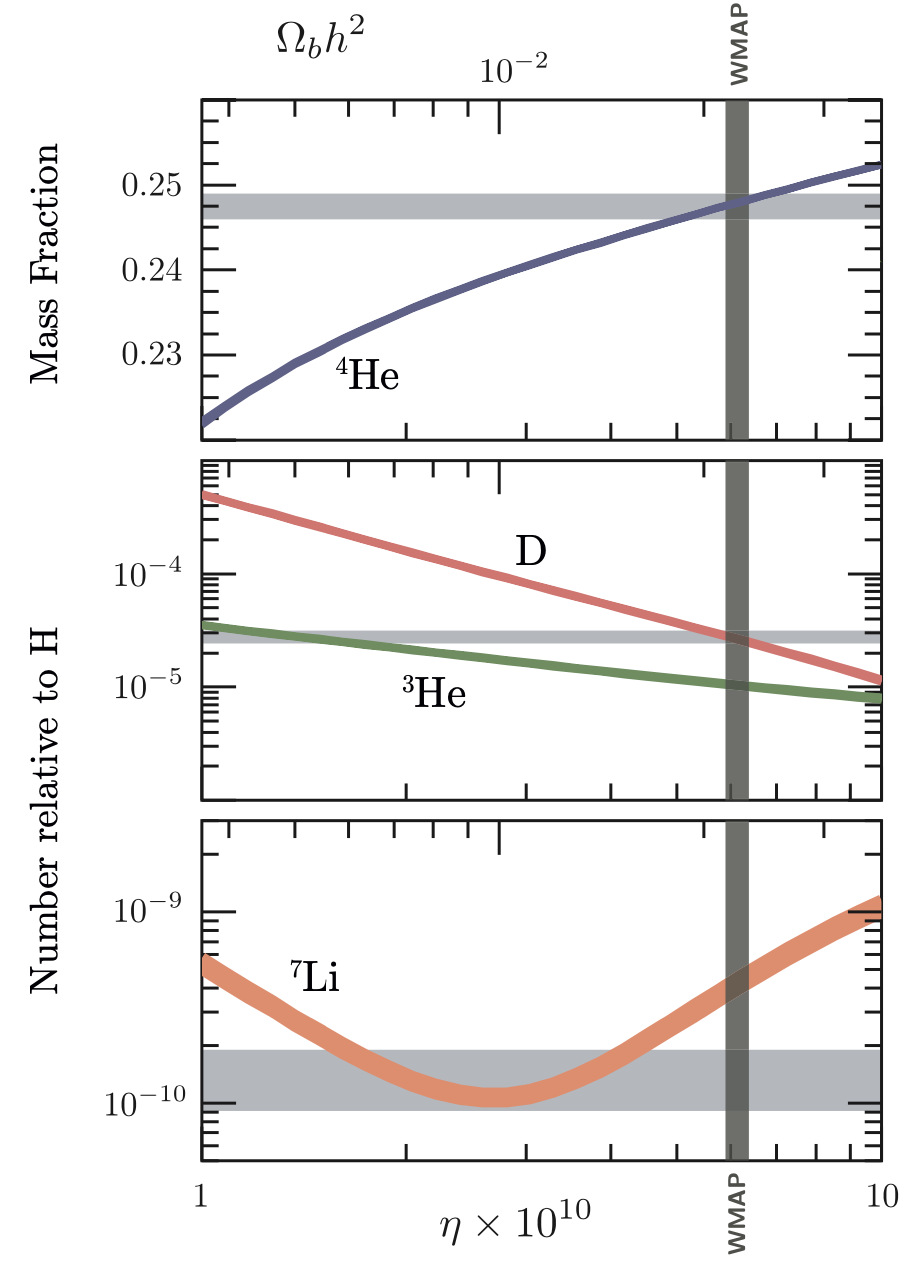
Figure 13:Comparaison entre les prédictions théoriques pour les abondances des noyaux légers (bandes colorées) et les mesures (bandes grises) (d’après Baumann (2022)).
Recombinaison¶
Dans l’univers primordial, la recombinaison se compose de deux étapes. D’abord il y a la formation des atomes d’hydrogène, puis le découplage des électrons libres restants et des photons. A ce moment là, le plasma se transforme en gaz d’hydrogène et d’hélium (plus un peu de lithium etc) neutre. Après la recombinaison, les photons du bain thermique sont libres de se propager dans l’Univers puisque le milieu est (quasi) neutre. Cette première lumière correspond au fond diffus cosmologique et nous renseigne sur l’état de l’Univers jeune et la physique qui s’y est déroulée avant (et après).
Formation des atomes d’hydrogène¶
La formation des atomes d’hydrogène se déroule par la réaction :
et on rappelle que l’énergie de liaison de l’hydrogène vaut . Une rapide approximation nous donnerait que la température à laquelle a eu lieu la recombinaison est , mais ce serait oublier qu’avec un milliard de photons pour un baryon, même à des températures plus basses l’Univers contient encore énormément de photons d’énergie assez haute pour ioniser les atomes d’hydrogène (queue de la distribution du corps noir). Ce qu’il faut, c’est donc trouver la température pour laquelle l’intégrale de la distribution de corps noir à des énergies supérieures à donne une densité de photons comparable à . Le paramètre est donc un paramètre important qui doit intervenir dans l’estimation de la température à la recombinaison.
Une meilleure estimation doit donc reposer au moins sur le rapport baryon sur photon et . Comme pour l’abondance du deutérium, à l’équilibre on peut écrire :
avec [9] et . C’est l’équation de Saha. Posons la fraction d’électrons libres dans le plasma primordial :
Par des arguments de neutralité électrique et de conservation du nombre de particules, on a aussi :
en supposant qu’il n’y a que de l’hydrogène pour simplifier les calculs (on ne considère par la recombinaison de l’hélium[10]). Par conséquent, on a :
et simplement :
donc :
On a une équation du second degré en , faisant intervenir , dont la solution est (Ryden (2017) p.192) :
On définit le moment de la recombinaison comme celui où le milieu est à moitié ionisé soit ou . Alors la température du découplage est donnée par Ryden, 2017 :
soit quand l’Univers est agé de ans et alors que son évolution est dorénavant dominée par son contenu en matière. D’après la Figure 15, on voit toutefois que la recombinaison s’étend globalement entre les redshift 1200 et 1600, ce qui correspond tout de même à environ ans, ce n’est donc pas un processus instantané pour nous humains, mais quand même rapide comparé à l’âge de l’Univers.
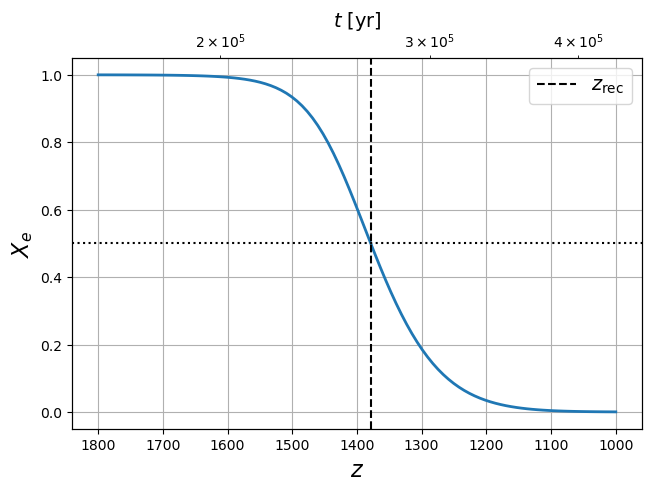
Figure 15:Fraction d’ionisation en fonction du redshift pendant la recombinaison.
Découplage des photons¶
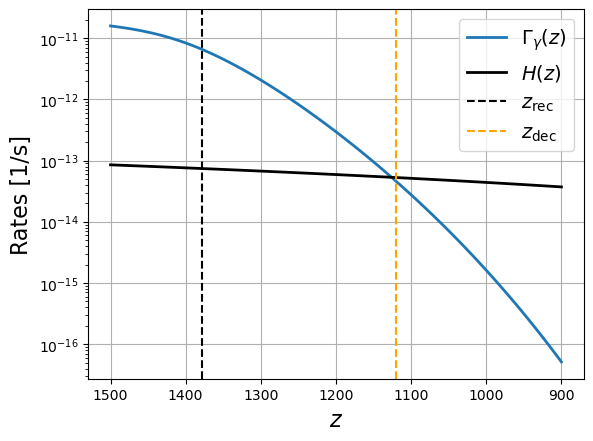
Figure 16:Comparaison entre le taux d’interaction et le taux d’expansion en fonction du redshift.
Pendant encore un certain temps après , les photons restent couplés à la petite fraction d’électrons libres restants par la diffusion Thomson :
Le taux d’interaction est donné par (voir équation (21)) :
avec la section efficace de la diffusion Thomson :
Le découplage a lieu lorsque ce taux d’interaction devient petit devant le taux d’expansion de l’Univers (Figure 16), soit :
L’Univers étant alors dominé par la matière (), on a :
On aboutit à :
Par une résolution numérique, on obtient :
Libre parcours moyen des photons
Une autre façon de voir le découplage entre photon et matière et donc le moment où l’Univers devient transparent, est de regarder le libre parcours moyen des photons . Loin dans le passé de l’Univers, celui-ci était opaque mais le libre parcours moyen des photons pouvait tout de même être de l’ordre de quelques années-lumières. Après le découplage, celui-ci devient supérieur à la taille typique de l’Univers.
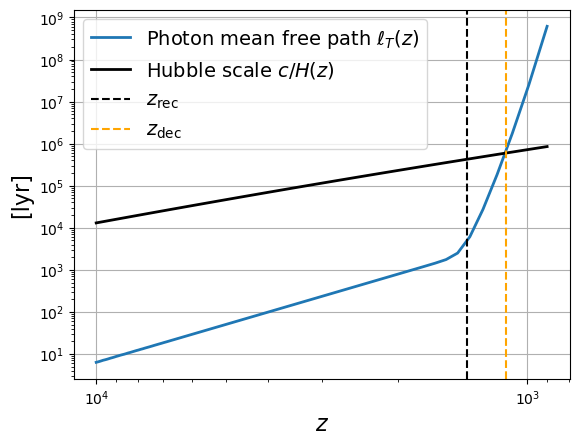
Figure 17:Comparaison entre le temps de libre parcours moyen des photons et le temps de Hubble .
Le fond diffus cosmologique est donc un rayonnement de corps noir qui a été libéré environ ans après le Big Bang, quand l’Univers n’était quasiment plus ionisé puisque .
les hadrons se scindent en deux familles : les mésons (2 quarks) et les baryons (3 quarks). On rappelle que parmi les baryons seuls les protons sont stables. Les neutrons liés dans les noyaux atomiques sont stables, mais libres ils se désintègrent en proton avec un temps de demie vie de 15 minutes. Les mésons sont tous instables avec des temps de demie vie plus courts que s.
la limite classique apparaît pour des très faibles nombres d’occupation des niveaux d’énergie, où la nature bosonique ou fermionique des particules n’a plus d’importance puisque . Elle est valable à faible densité ou à haute température, lorsque la condition suivante est vérifiée : , où est la distance moyenne entre particules et est la longueur d’onde thermique de De Broglie.
dès 1ns après le Big Bang, le seul boson survivant est le photon car les bosons , et se désintègrent. De plus, lors de leur apparition lors de la transition électrofaible vers GeV, leurs masses sont telles qu’ils sont déjà trop lourds pour être relativistes. Il n’y a donc guère que les photons à considérer dans la liste des bosons relativistes, dont le potentiel chimique est nul à l’équilibre thermodynamique.
puisque la charge électrique est associée aux forces de Coulomb et que l’expansion de l’Univers n’est gouvernée que par les forces gravitationnelles, l’Univers doit être globalement neutre.
stricto sensus une constante d’intégration entropique doit apparaître mais celle-ci est nulle en vertu du troisième principe de la thermodynamique.
on rappelle que les masses des protons et neutrons sont d’environ .
le noyau d’hélium 4 possède un nombre dit magique de neutrons et protons (Magic number (physics)) qui le stabilise et lui confère une énergie de liaison bien supérieure au deutérium ou au lithium, ses voisins dans le tableau périodique des éléments.
un atome d’hydrogène peut avoir un spin 0 (spins inversés) ou 1 (spins alginés) donc 4 degrés de liberté internes.
avec un neutron pour 7 protons, donc en nombre plus de des baryons sont des protons.
- Planck Collaboration, Aghanim, N., Akrami, Y., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., Banday, A. J., Barreiro, R. B., Bartolo, N., Basak, S., Battye, R., Benabed, K., Bernard, J.-P., Bersanelli, M., Bielewicz, P., Bock, J. J., Bond, J. R., Borrill, J., … Zonca, A. (2020). Planck 2018 results - VI. Cosmological parameters. A&A, 641, A6. 10.1051/0004-6361/201833910
- Rubin, V. C., & Ford, W. Kent, Jr. (1970). Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. The Astrophysical Journal, 159, 379. 10.1086/150317
- Alpher, R. A., & Herman, R. (1948). Evolution of the Universe. Nature, 162(4124), 774–775. 10.1038/162774b0
- Gamow, G. (1948). The Evolution of the Universe. Nature, 162(4122), 680–682. 10.1038/162680a0
- Penzias, A. A., & Wilson, R. W. (1965). A Measurement of Excess Antenna Temperature at 4080 Mc/s. The Astrophysical Journal, 142, 419. 10.1086/148307
- Penzias, A. A., & Wilson, R. W. (1965). Measurement of the Flux Density of CAS a at 4080 Mc/s. The Astrophysical Journal, 142, 1149. 10.1086/148384
- Fixsen, D. J. (2009). The temperature of the cosmic microwave background. The Astrophysical Journal, 707(2), 916–920. 10.1088/0004-637X/707/2/916
- Condon, J. J., & Matthews, A. M. (2018). ΛCDM Cosmology for Astronomers. Publications of the Astronomical Society of the Pacific, 130(989), 073001. 10.1088/1538-3873/aac1b2
- Mather, J. C., Fixsen, D. J., Shafer, R. A., Mosier, C., & Wilkinson, D. T. (1999). Calibrator Design for the COBE Far-Infrared Absolute Spectrophotometer (FIRAS). The Astrophysical Journal, 512(2), 511–520. 10.1086/306805
- Hurier, G., Aghanim, N., Douspis, M., & Pointecouteau, E. (2014). Measurement of theTCMBevolution from the Sunyaev-Zel’dovich effect. Astronomy & Astrophysics, 561, A143. 10.1051/0004-6361/201322632
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & López, S. (2011). The evolution of the cosmic microwave background temperature: Measurements ofTCMBat high redshift from carbon monoxide excitation. Astronomy & Astrophysics, 526, L7. 10.1051/0004-6361/201016140
- Kolb, E. W., & Turner, M. S. (1990). The Early Universe (Vol. 69). 10.1201/9780429492860
- Weinberg, S. (1989). The cosmological constant problem. Reviews of Modern Physics, 61(1), 1–23. 10.1103/RevModPhys.61.1
- ParticleDataGroup, Workman, R. L., Burkert, V. D., Crede, V., Klempt, E., Thoma, U., Tiator, L., Agashe, K., Aielli, G., Allanach, B. C., Amsler, C., Antonelli, M., Aschenauer, E. C., Asner, D. M., Baer, H., Banerjee, S., Barnett, R. M., Baudis, L., Bauer, C. W., … Zyla, P. A. (2022). Review of Particle Physics. Progress of Theoretical and Experimental Physics, 2022(8), 083C01. 10.1093/ptep/ptac097
- Peebles, P. J. E. (1966). Primordial Helium Abundance and the Primordial Fireball. II. \apj, 146, 542. 10.1086/148918